Derivative Of The Natural Log Function

Derivatives of logarithmic functions

Derivatives of logarithmic functions are fundamental in calculus. They provide a way to find the rate of change of a logarithmic function. There are two main forms to consider: the natural logarithm and logarithms with other bases.

The following are the formulas for the derivatives of logarithmic functions:

 

Logarithm Worksheets
Practice your skills with the following worksheets:
Printable & Online Logarithm Worksheets

1. Natural Logarithm:
   \(\frac{d}{dx}\left( \text{ln }x \right)=\frac{1}{x}\)
   
2. Natural Logarithm with Chain Rule:
   \(\frac{d}{dx}\left( \text{ln }u \right)=\frac{1}{u}\cdot \frac{du}{dx} \)
   
3. Logarithm with Base a:
   \(\frac{d}{dx}\left( \text{log}_ax \right)=\frac{1}{x\text{ ln }a}\)
   
4. Logarithm with Base a and Chain Rule:
   \(\frac{d}{dx}\left( \text{log}_au \right)=\frac{1}{u\text{ ln }a} \cdot \frac{du}{dx} \)

Natural Log (ln)

The Natural Log is the logarithm to the base e, where e is an irrational constant approximately equal to 2.718281828. The natural logarithm is usually written ln(x) or log_e(x).

The natural log is the inverse function of the exponential function. They are related by the following identities:
e^ln(x) = x
ln(e^x) = x

Derivative Of ln(x)

Using the Chain Rule, we get

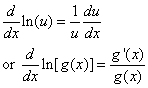
Example:
Differentiate y = ln(x² +1)

Solution:
Using the Chain Rule, we get

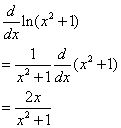
Example:
Differentiate

Solution:

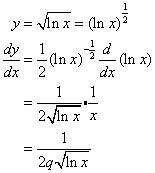
Derivatives Of Logarithmic Functions

The derivative of the natural logarithmic function (ln[x]) is simply 1 divided by x. This derivative can be found using both the definition of the derivative and a calculator. Derivatives of logarithmic functions are simpler than they would seem to be, even though the functions themselves come from an important limit in Calculus.

What Are The Formulas For Finding Derivatives Of Logarithmic Functions And How To Use Them To Find Derivatives?

Examples:
Find the derivatives for the following logarithmic functions:

1. f(x) = ln(x² + 10)
2. f(x) = √x ˙ ln(x)
3. f(x) = ln[(2x + 1)³/(3x - 1)⁴]
4. y = [log_a(1 + e^x)]²

• Show Video Lesson

Derivatives Of Logarithmic Functions

Find the derivatives for the following logarithmic functions:

Examples:

1. y = ln(x² x)
2. y = (log₇ x)^1/3
3. y = ln(x⁴˙sin x)
4. y = lnx/[1 + ln(2x)]

• Show Video Lesson

Derivatives Of The Natural Log Function (Basic)

How to differentiate the natural logarithmic function?

Examples:
Determine the derivative of the function.

1. f(x) = 2ln(x)
2. f(x) = ln(4x)

• Show Video Lesson

Derivatives Of The Natural Log Function With The Chain Rule

How to differentiate the natural logarithmic function using the chain rule?

Example:
Determine the derivative of the function.
f(x) = 5ln(x³)

• Show Video Lesson

The Derivative Of The Natural Log Function

We give two justifications for the formula for the derivative of the natural log function. If you want to see where this formula comes from, this is the video to watch.

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.