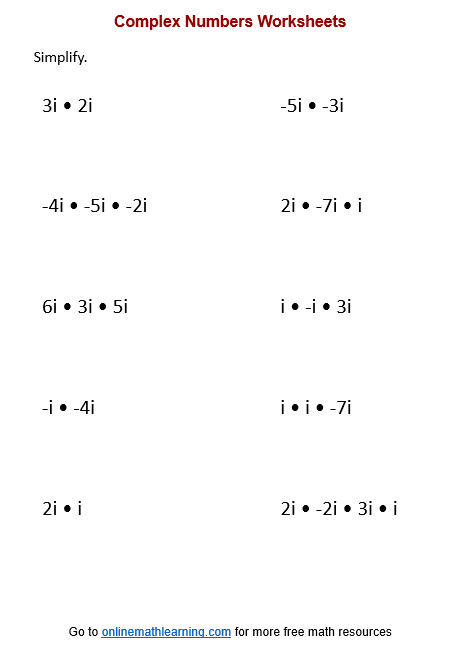Complex Number Worksheets

Printable complex numbers worksheets:
Add & Subtract Complex Numbers
Multiply Complex Number
Rationalize Complex Number
Operations with Complex Numbers
Quadratic Equation with Complex Solutions

Examples, solutions, videos, and worksheets to help Algebra II students learn how to multiply complex numbers.

How to multiply complex numbers?

There are three sets of multiply complex numbers worksheets

• Multiply Complex Numbers (Monomials)
• Multiply Complex Numbers (Monomials & Binomials)
• Multiply Complex Numbers (Binomials)

In mathematics, the imaginary unit i is defined as the square root of -1. It is a fundamental concept in complex numbers. Powers of i repeat in a cyclic pattern, which makes them predictable. Here are the powers of i up to i⁵:

1. i¹ = i
2. i² = -1 (since i is square root of -1)
3. i³ = -i (since i³ is the product of i² and i)
4. i⁴ = 1 (since i⁴ is the square of -1)
5. i⁵ = i (since i⁵ is the product of i⁴ and i) The pattern repeats from i⁵. i⁶ = i² and so on.
   

Multiply binomial complex numbers
To multiply binomial complex numbers, you use the distributive property of multiplication over addition.

Here’s how you multiply two complex numbers (a + bi) and (c + di)

Distribute each term in the first binomial to each term in the second binomial:
(a + bi) · (c + di)
= a · c + a · di + c · bi + bi · di
= ac + adi + bci + bdi²
= ac + adi + bci - bd
= ac - bd + (ad + bc)i

Example:
Multiply (2 + 3i) by (1 − 4i):

Use the distributive property to multiply the terms:
(2 + 3i) · (1 − 4i)
= (2 · 1) + (2 · -4i) + (3i · 1) + (3i · - 4i)
= 2 - 8i + 3i - 12i²
= 2 - 5i - (-12)
= 14 - 5i

Have a look at this video if you need to review how to multiply complex numbers.

• Multiplying Complex Numbers

Click on the following worksheet to get a printable pdf document.
Scroll down the page for more Complex Number Worksheets.

 

More Complex Number Worksheets

Printable
(Answers on the second page.)
Complex Number Worksheet #1 (Monomials)
Complex Number Worksheet #2 (Monomials & Binomials)
Complex Number Worksheet #3 (Binomials)

Online
Powers of i: Positive Exponents
Powers of i: Negative Exponents
Complex Number Addition
Complex Number Subtraction
Complex Number Multiplication
Complex Number Division

Complex Number: Magnitude (Absolute Value)
Distance Between Two Complex Numbers
Midpoint of Two Complex Numbers)

Related Lessons & Worksheets

Add & Subtract Complex Number

More Printable Worksheets

Check out our most popular games!
Fraction Concoction	Fact Family Game	Number Bond Garden
Online Addition Subtraction Game	Penguin Solitaire	Sawayama Solitaire
Ark Solitaire	Eldritch Invasion	Shenzhen Solitaire

Check out more Solitaire games here.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.