AP Calculus AB 2016 Questions And Answers
Related Pages
AP Calculus AB 2018 Exam
AP Calculus AB 2017 Exam
Calculus Lessons
Questions And Worked Solutions For AP Calculus AB 2016
AP Calculus AB 2016 Free Response Questions - Complete Paper (pdf)
AP Calculus AB 2016 Free Response Question 1
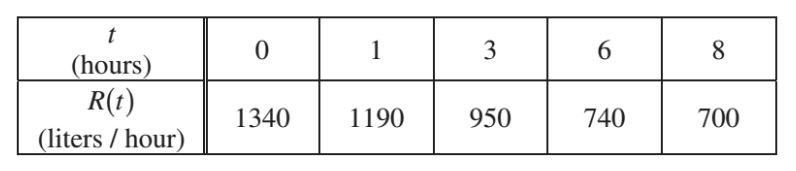
- Water is pumped into a tank at a rate modeled by W(t) = 2000e-t2/20 liters per hour for 0 ≤ t ≤ 8, where t is measured in hours. Water is removed from the tank at a rate modeled by R(t) liters per hour, where R is differentiable and decreasing on 0 ≤ t ≤ 8. Selected values of R(t) are shown in the table above. At time t = 0, there are 50,000 liters of water in the tank.
(a) Estimate R'(2). Show the work that leads to your answer. Indicate units of measure.
(b) Use a left Riemann sum with the four subintervals indicated by the table to estimate the total amount of water removed from the tank during the 8 hours. Is this an overestimate or an underestimate of the total amount of water removed? Give a reason for your answer.
(c) Use your answer from part (b) to find an estimate of the total amount of water in the tank, to the nearest liter, at the end of 8 hours.
(d) For 0 ≤ t ≤ 8, is there a time t when the rate at which water is pumped into the tank is the same as the rate at which water is removed from the tank? Explain why or why not.
AP Calculus AB 2016 Free Response Question 2
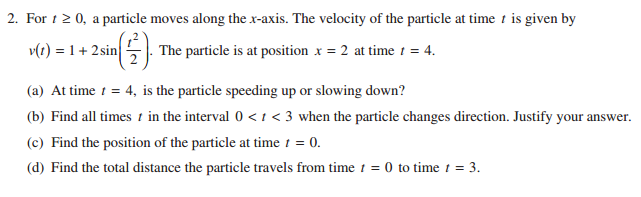
AP Calculus AB 2016 Free Response Question 3
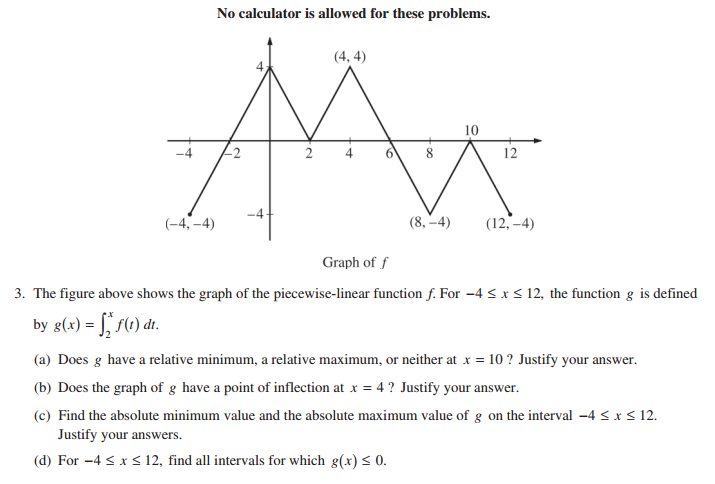
AP Calculus AB 2016 Free Response Question 4
AP Calculus AB 2016 Free Response Question 5
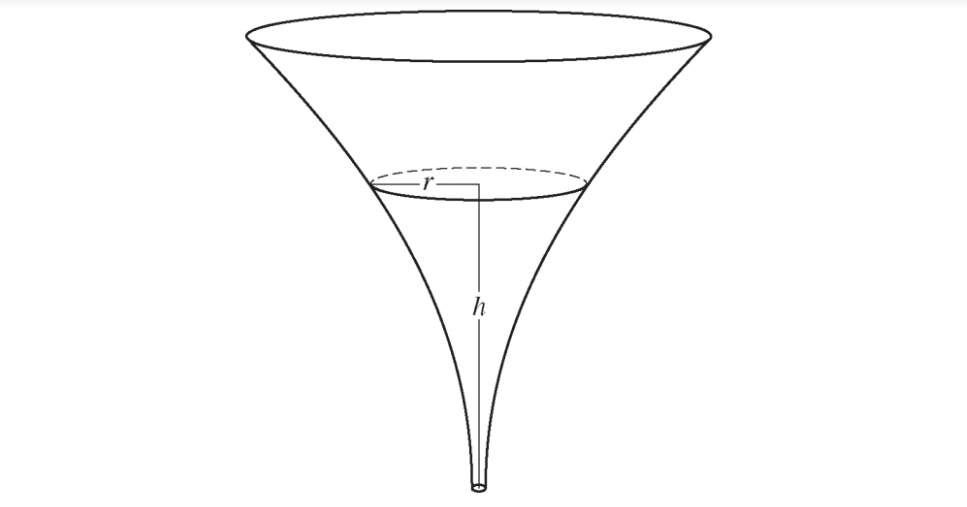
- The inside of a funnel of height 10 inches has circular cross sections, as shown in the figure above. At height h, the radius of the funnel is given by r = 1/20 (3 + h2), where 0 ≤ h ≤ 10. The units of r and h are inches.
(a) Find the average value of the radius of the funnel.
(b) Find the volume of the funnel.
(c) The funnel contains liquid that is draining from the bottom. At the instant when the height of the liquid is h = 3 inches, the radius of the surface of the liquid is decreasing at a rate of 1/5 inch per second. At this instant, what is the rate of change of the height of the liquid with respect to time?
AP Calculus AB 2016 Free Response Question 6
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.