Algebra Motion Problems
Related Pages
Rate, Time and Distance Word Problems
Rate, Time and Distance
More Algebra Word Problems
More Algebra Lessons
In these lessons, we will learn how to solve algebra word problems that involve motion. Motion word problems using algebra involve calculating distance, speed, or time, based on the relationships between these quantities. The key formula for motion problems is:
Distance = Speed × Time
What are Motion or Distance Word Problems?
Motion problems are based on the formula
d = rt
where d = distance, r = rate and t = time.
How to solve Motion or Distance Word Problems?
Step 1: Draw a diagram to represent the relationship between the distances involved in the problem.
Step 2: Set up a chart based on the formula: rate × time = distance.
Step 3: Use the chart to set up one or more equations.
Step 4: Solve the equations.
The following diagram gives the steps to solve an motion word problem using Algebra.
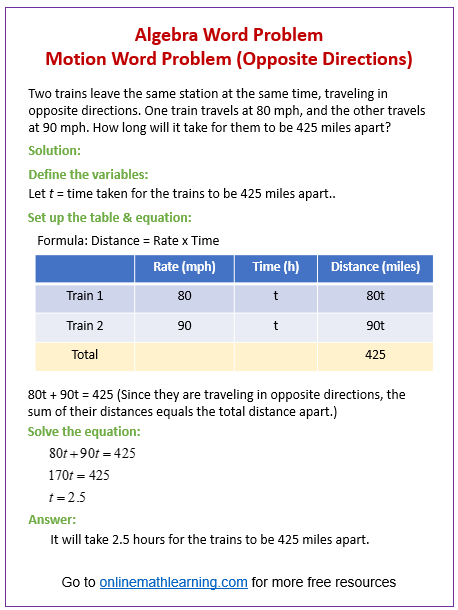
Motion/Distance Word Problems:
Travel in Same Direction
Travel in Opposite Directions
Round Trip Problems
Average Speed Problems
Wind/Current Problems
We will look at three types of Motion Word Problems:
- Two objects going in opposite directions.
- Both objects going in the same direction, but one goes further.
- One object going and returning at different rates.
Solve Motion Word Problems: Two objects going in opposite directions
Example:
John and Philip who live 14 miles apart start at noon to walk toward each other at rates of 3 mph and 4 mph
respectively. After how many hours will they meet?
Solution:
Let x = time walked.
| r | t | d | |
| John | 3 | x | 3x |
| Philip | 4 | x | 4x |
3x + 4x = 14
7x = 14
x = 2
They will meet in 2 hours.
How to solve motion word problems with objects traveling in opposite directions?
Example:
Two cars leave from the same place at the same time and travel in opposite direction. One car travels at 55 mph
and the other at 75 mph. After how many hours will there be 520 miles apart?
Example:
Two planes leave the same point at 8 AM. Plane 1 heads East at 600 mph and Plane 2 heads West at 450 mph.
How long will they be 1400 miles apart? At what time will they be 1400 miles apart? How far has each plane traveled?
Solve Motion Word Problems: Two objects going in the same direction
Example:
Aaron left L.A. to drive at 55 mph towards Las Vegas. Mike left L.A. an hour after Aaron (also towards Las Vegas),
driving at 70 mph. How long will it take Mike to overtake Aaron?
How to solve motion word problems with objects traveling in the same direction?
Example:
John left his house at 3.00 pm to drive 60 mph to drive towards Michigan. Phoebe left the same house at 5.00 pm,
driving 80 mph in the same direction as John. How long will it take Phoebe to overtake John?
Solve Motion Word Problems: One object going and returning at different rates
Example:
In still water, Peter’s boat goes 4 times as fast as the current in the river. He takes a 15-mile trip up the
river and returns in 4 hours. Find the rate of the current.
Solution:
Let x = rate of the current.
| r | t | d | |
| down river | 4x + x | 15 / 5x | 15 |
| up river | 4x - x | 15 / 3x | 15 |
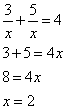
The rate of the current is 2 mph.
Example:
Gordon rode his bike at 15 mph to get his car. He then drove back at 45 mph. If the entire trip took him 8
hours, how far away was his car?
Motion Word Problems
This is how to set up motion problems for Algebra.
Three Types of Problems
- Both going the same direction but one going further
- Two going in opposite directions
- Going in one direction and then returning at a different rate.
Check out many other Algebra Word Problems
Age Word Problems, Average Word Problems, Coin Word Problems, Consecutive Integer Word Problems, Digit Word Problems, Distance Word Problems, Fraction Word Problems, Geometry Word Problems, Integer Word Problems, Interest Word Problems, Lever Word Problems, Mixture Word Problems, Money Word Problems, Motion & Distance Word Problems, Number Sequence Word Problems, Proportion Word Problems, Quadratic Equation Word Problems, Ratio Word Problems, Symbol Word Problems, Variation Word Problems, Work Word Problems.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.