Vector Subtraction
Related Pages
Vectors
Equal Vectors
Vector Addition
Vector Multiplication
Vector Geometry
In this lesson, we will learn how to subtract vectors by adding its negative, how to subtract vectors geometrically using the head-to-tail method and how to subtract vectors using their components.
What is a vector?
A vector is a quantity that has magnitude (size) and direction.
How to represent a vector graphically, in column-vector form and in unit-vector form?
How to subtract Vectors?
Vector subtraction is the operation of finding the difference between two vectors. Subtracting a vector v from a vector u (written as u - v) is equivalent to adding the negative of vector v to vector u (u + (-v)).
The following diagram shows how to subtract vectors graphically. Scroll down the page for more examples and solutions for vector subtraction.
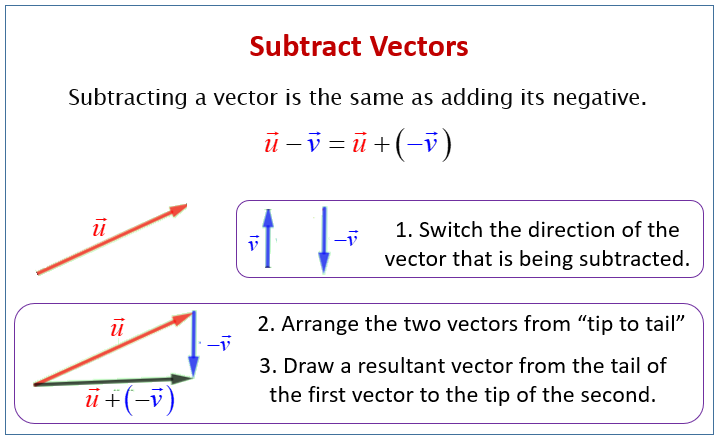
Subtracting a vector is the same as adding its negative. The negative of a vector has the same magnitude (length) as the original vector but points in the opposite direction.
The difference of the vectors p and q is the sum of p and –q.
p – q = p + (–q)
Geometric Method (Head-to-Tail or Triangle Law):
- Draw the first vector p starting from an initial point.
- Draw the negative of the second vector -q starting from the tail (arrow tip) of the first vector p. Remember to reverse the direction of -q while keeping its length the same.
- The resultant vector p - q is the vector drawn from the head of the first vector p to the tail of the negative of the second vector -q.
Example:
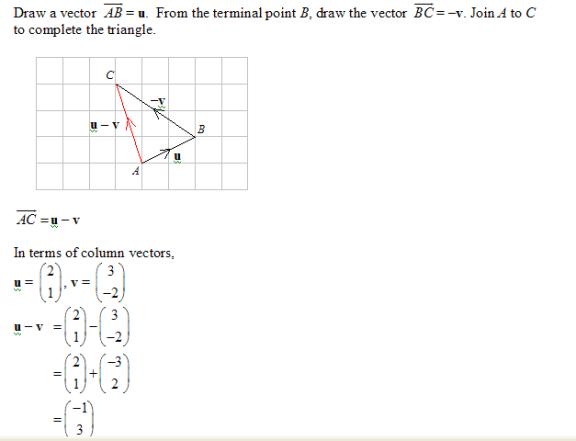
Subtract the vector v from the vector u.
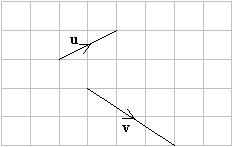
-
Show Solution
u – v = u + (–v)
Change the direction of vector v to get the vector –v.

Check: The column vector should represent the vector that was drawn.
How to subtract vectors using column vectors?
u - v = u + (-v)
Since we know how to add vectors and multiply by negative one, we can also subtract vectors.
How to subtract vectors using column vectors and explained graphically?
How to subtract vectors graphically?
Geometric subtraction of two vectors
How to solve word problems using vector subtraction?
Vector word problems when given magnitude and direction
Subtract the following vectors (B - A)
A = 5.0 m at 40 degrees west of North
B = 2.5 m south.
Find the distance and direction of (B - A)
Vector subtraction including boat example
Introduction to ‘head to tail’ vector subtraction in the geometric sense. This is then applied to an example of working out a boat’s velocity relative to water given the velocity of the current and the velocity of the boat relative to land are both known.
velocity relative to land = water velocity + boat’s velocity relative to water.
Example:
A woman wants to get to a destination that is due North of her starting point. To do this, she needs to row across a stream. The current is flowing East at 12km/hr. The woman can row the boat at a constant speed of 16km/hr.
What will be the required direction that she must row the boat in order to reach the required destination?
How to subtract vectors using their components
Subtracting Vectors in Component Form for 2-D and 3-D vectors.
How to add and subtract vectors in component form?
Example:
Let u = <-1, 3>, v = <2, 4>, and w = <2, -5>. Find the component form of the vector
u + v
u - w
2u + 3w
2u - 4v
-2u - 3v
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.