Applications Of Trigonometry
In these lessons, we will learn how to apply trigonometry to solve different types of word problems.
Related Pages
Trigonometry Word Problems
Lessons On Trigonometry
Inverse trigonometry
Trigonometry Worksheets
Hints On Solving Word Problems Or Applications Of Trigonometry:
- If no diagram is given, draw one yourself.
- Mark the right angles in the diagram.
- Show the sizes of the other angles and the lengths of any lines that are known
- Mark the angles or sides you have to calculate.
- Consider whether you need to create right triangles by drawing extra lines. For example, divide an isosceles triangle into two congruent right triangles.
- Decide whether you will need Pythagorean theorem, sine, cosine or tangent.
- Check that your answer is reasonable. For example, the hypotenuse is the longest side in a right triangle.
Example:
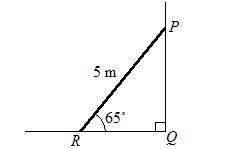
A ladder 5 m long, leaning against a vertical wall makes an angle of 65˚ with the ground.
a) How high on the wall does the ladder reach?
b) How far is the foot of the ladder from the wall?
c) What angle does the ladder make with the wall?
Solution:
a) The height that the ladder reach is PQ
PQ = sin 65˚ × 5 = 4.53 m
b) The distance of the foot of the ladder from the wall is RQ.
RQ = cos 65˚ × 5 = 2.11 m
c) The angle that the ladder makes with the wall is angle P
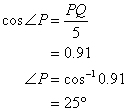
Videos
The following videos shows more examples of solving application of trigonometry word problems.
Example 1: Suppose that a 10 meter ladder is leaning against a building such that the angle of elevation from ground to the building is 62 degrees. Find the distance of the foot of the ladder from the wall. Also, find the distance from the ground to the top of the ladder.
Example 2: Suppose that from atop a 100m vertical cliff a ship is spotted at an angle of depression of 12 degrees. How far is the ship from the base of the cliff? Also, find the distance from the top of the cliff to the ship.
Trigonometry Word Problem
How to Find The Height of a Building using trigonometry?
Example:
A hiker is hiking up a 12 degrees slope. If he hikes at a constant rate of 3 mph,
how much altitude does he gain in 5 hours of hiking?
Example:
A balloon is hovering 800 ft above a lake. The balloon is observed by the crew of a boat as they look upwards
at an angle of 20 degrees. Twenty-five seconds later, the crew has to
look at angle of 65 degrees to see the balloon. How fast was the boat traveling?
Trigonometry word problems (part 1)
Navigation Problem: The first part of a problem when the captain of a ship goes off track.
Trigonometry word problems (part 2)
The second part of the problem of the off-track ship captain.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.