Trigonometric Word Problems
Related Pages
Trigonometry Word Problems
Lessons On Trigonometry
Inverse trigonometry
Trigonometry Worksheets
In these lessons, examples, and solutions we will learn the trigonometric functions (sine, cosine, tangent) and how to solve word problems using trigonometry.
How to Solve Trigonometry Word Problems?
Trigonometry word problems use sine, cosine, tangent, and the Pythagorean theorem to solve real-world scenarios involving angles and distances. Here are some steps to help you solve these problems:
-
Understand the Problem
Identify what’s given (angles, sides, measurements) and what’s asked.
Draw a diagram to visualize the scenario (e.g., a right triangle, a ramp, a ladder leaning on a wall).
You may need to create right triangles by drawing extra lines. For example, divide an isosceles triangle into two congruent right triangles.
Mark the right angles in the diagram.
Write in the sizes of the other angles and the lengths of any lines that are known.
Mark the angles or sides you have to calculate. -
Label the Triangle
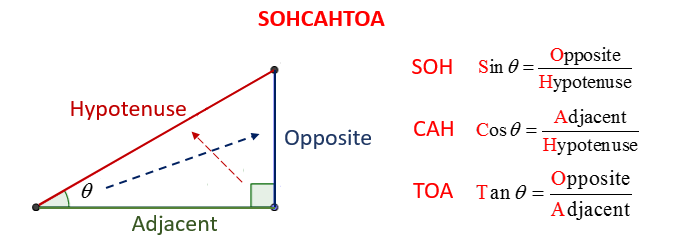
Hypotenuse (H): Longest side (opposite the right angle).
Opposite (O): Side opposite the given angle.
Adjacent (A): Side next to the given angle. -
Choose the Correct Trig Function
Decide whether you will need the Pythagorean theorem, sine, cosine or tangent.
Use SOH-CAH-TOA to decide which ratio to apply:
Sine (sinθ) = Opposite / Hypotenuse (O/H)
Cosine (cosθ) = Adjacent / Hypotenuse (A/H)
Tangent (tanθ) = Opposite / Adjacent (O/A)
The following diagram shows how SOHCAHTOA can help you remember how to use sine, cosine, or tangent to find missing angles or missing sides in a trigonometry problem. Scroll down the page for examples and solutions.
Printable & Online Trigonometry Worksheets
-
Set Up the Equation & Solve
-
Check that your answer is reasonable.
How To Use Cosine To Calculate The Side Of A Right Triangle?
Example:
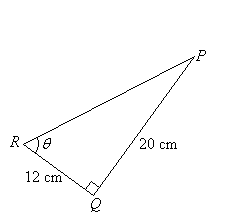
Calculate the value of cosθ in the triangle.
Solution:
Use the Pythagorean theorem to evaluate the length of PR.
![]()
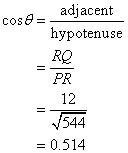
How To Use Tangent To Calculate The Side Of A Triangle?
Example:
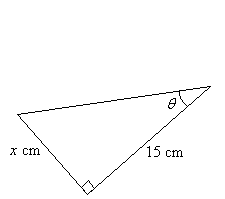
Calculate the length of the side x, given that tan θ = 0.4
Solution:
![]()
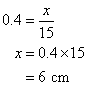
How To Use Sine To Calculate The Side Of A Triangle?
Example:
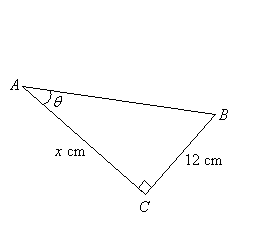
Calculate the length of the side x, given that sin θ = 0.6
Solution:
![]()
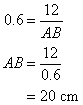
Using the Pythagorean theorem:
![]()
How To Solve Word Problems Using Trigonometry?
The following video shows how to use the trigonometric ratio, tangent, to find the height of a balloon.
How To Solve Word Problems Using Sine?
This video shows how to use the trigonometric ratio, sine, to find the elevation gain of a hiker going up a slope.
Example: A hiker is hiking up a 12 degrees slope. If he hikes at a constant rate of 3 mph, how much altitude does he gain in 5 hours of hiking?
How To Use Cosine To Solve A Word Problem?
Example: A ramp is pulled out of the back of truck. There is a 38 degrees angle between the ramp
and the pavement. If the distance from the end of the ramp to to the back of the truck
is 10 feet. How long is the ramp?
Step 1: Find the values of the givens.
Step 2: Substitute the values into the cosine ratio.
Step 3: Solve for the missing side.
Step 4: Write the units
How To Solve Word Problems Using Tangent?
The following video shows how to use trigonometric ratio, tangent, to find the height of a building.
How To Solve Trigonometry Word Problems Using Tangent?
Example: Neil sees a rocket at an angle of elevation of 11 degrees. If Neil is located at 5 miles from the rocket launch pad, how high is the rocket?
How To Determining The Speed Of A Boat Using Trigonometry?
Example: A balloon is hovering 800 ft above a lake. The balloon is observed by the crew of a boat as they look upwards at an angle of 0f 20 degrees. 25 seconds later, the crew had to look at an angle of 65 degrees to see the balloon. How fast was the boat traveling?
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.