Trigonometry: Evaluating Angles

Special Angles

The “special angles” in trigonometry are angles for which the trigonometric functions (sine, cosine, tangent, etc.) have values that can be expressed exactly using simple fractions and radicals (square roots). These angles are significant because they appear frequently in mathematical problems and applications. The most common special angles are 0°, 30°, 45°, 60°, and 90°.

How to find Trig Ratios of special angles?
We will first look into the trigonometric functions of the angles 30°, 45° and 60°. You can find the trigonometric ratios of special angles (0°, 30°, 45°, 60°, 90°) using special right triangles: 30°-60°-90° Triangle and 45°-45°-90° Triangle.

Trig Ratios for 30° and 60°
Let us consider 30° and 60°.
These two angles form a 30°-60°-90° right triangle as shown.
The ratio of the sides of the triangle is
1 : √3 : 2

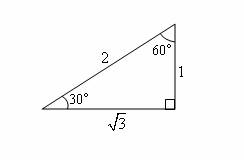
From the triangle we get the ratios as follows:

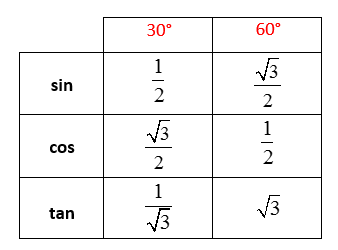
Trig Ratio for 45°
Next, we consider the 45˚ angle that forms a 45°-45°-90° right triangle as shown. The ratio of the sides of the triangle is

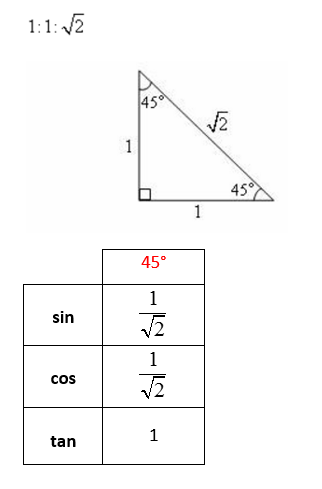
Combining the two tables we get:

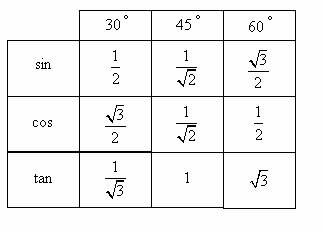
Trigonometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Trigonometry Worksheets

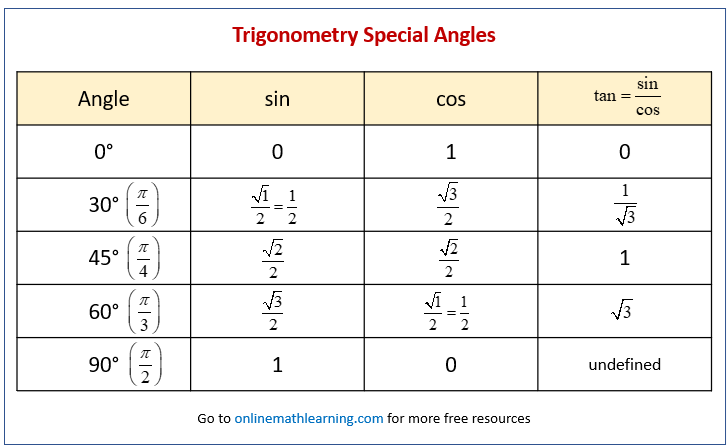
Trig Table for Special Angles
One way to remember the trig values for special angles is to set up a table.

Notice this pattern in the table:
For sine, the numbers under the square root go from 1 to 3.
For cosine, the numbers under the square root go from 3 to 1.
Once you have sine and cosine, you can find tangent using the identity \(tan = \frac{sin}{cos}\).

Example:
Evaluate the following without using a calculator:
a) 2 sin 30˚ + 3 cos 60˚ – 3 tan 45˚
b) 3(cos 30˚)² + 2 (sin 30˚ )²

Solution:
a) 2 sin 30˚ + 3 cos 60˚ – 3 tan 45˚

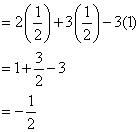
b) 3(cos 30˚)² + 2 (sin 30˚)²

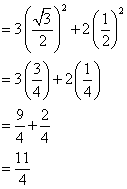
How to find the trig ratios of the special angles?
Using a 45-45-90 triangle and a 30-60-90 triangle find sine, cosine and tangent values of 0, 30, 45, 60 and 90 degrees

• Show Video Lesson

Find exact values of expressions involving sine, cosine and tangent values of 0, 30, 45, 60 and 90 degrees

Example:
Determine the exact values of each of the following:
a) sin30°tan45° + tan30°sin60°
b) cos30°sin45° + sin30°tan30°

• Show Video Lesson

How To Use A Calculator To Find Trig Ratios And Angles?

We could make use of a scientific calculator to obtain the trigonometric value of an angle. (Your calculator may work in a slightly different way. Please check your manual.)

Example:
Find the value of cos 6.35˚.

Solution:
Press

<cos 6.35˚ = 0.9939 (correct to 4 decimal places)

Example:
Find the value of sin 40˚ 32’.

Solution:

sin 40˚ 32’ = 0.6499 (correct to 4 decimal places)

Example:
Find the value of x for the following triangle. (Give your answer correct to 4 decimal places)

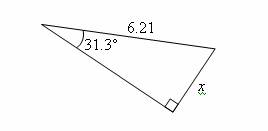
Solution:

x = 6.21 × sin 31.3˚ = 3.2262

Finding trig ratios and angles using your calculator

Examples:

1. Use a calculator to find the function value. Use the correct number of significant digits.
   a) cos 369.18°
   b) tan 426,62°
   c) sin 46.6°
   d) cot 17.9°

2. Determine θ in degrees. Use the correct number of significant digits.
   a) sin θ = 0.42
   b) cos θ = 0.29
   c) tan θ = 0.91

3. Determine θ in decimal degrees, 0° ≤ θ ≤ 90°. Use the correct number of significant digits.
   a) csc θ = 3.6
   b) cot θ = 2.1
   c) csc θ = 1.63
   d) sec θ = 7.25

• Show Video Lesson

Determining Trigonometric Function Values on the Calculator

Using the TI 84 to find function values for sine, cosine, tangent, cosecant, secant, and cotangent.

Examples:

1. sin 30°
2. cos 45°
3. tan(-264°)
4. sec(102.5°)
5. csc(432°)
6. cot(-23.45°)

• Show Video Lesson

Inverse Trigonometric Functions

We can use inverse trigonometric functions to find an angle with a given trigonometric value. We can also inverse trigonometric functions to solve a right triangle.

Examples:

1. Use the calculator to find an angle θ in the interval [0, 90] that satisfies the equation.
   a) sin θ = 0.7523
   b) tan θ = 3.54

2. Solve the given right triangle if a = 44.3 cm and b = 55.9 cm

3. Find each angle in a 3, 4, 5 right triangle.

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.