Trigonometric Ratios of Special Angles: 0°, 30°, 45°, 60°, 90°

How To Derive And Memorize The Trigonometric Ratios Of The Special Angles: 30°, 45° And 60°?

The following special angles chart show how to derive the trig ratios of 30°, 45° and 60° from the 30-60-90 and 45-45-90 special triangles. Scroll down the page if you need more examples and explanations on how to derive and use the trig ratios of special angles.

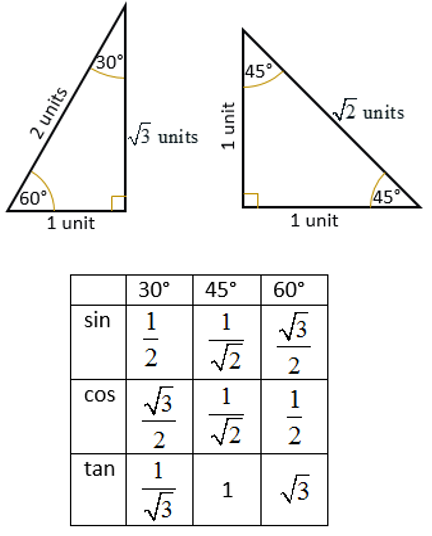
• Trigonometry Worksheets

  Printable
  Trig Ratios: Sin, Cos, Tan
  Sin & Cos of Complementary Angles
  Find Missing Sides
  Find Missing Angles
  Area of Triangle using Sine
  Law of Sines and Cosines
  

  Online
  Trigonometry (sine, cosine, tangent)
  Trigonometry (sine, cosine, tangent)
  Trigonometry (using a calculator)
  Inverse Trigonometry (using a calculator)
  Trigonometry (find an unknown side)
  Trigonometry (find an unknown angle)
  
  Using Sine
  Using Cosine
  Using Tangent
  Using Sine, Cosine or Tangent
  
  Trigonometry Applications Problems
  

1. Using 45°-45°-90° Special Right Triangle:
   Consider a right-angled isosceles triangle with two equal sides of length 1. By the Pythagorean theorem, the hypotenuse has a length of \(\sqrt{1^2 + 1^2} = \sqrt{2}\).
   The angles are 45°, 45°, and 90°.
   Using the definitions of trigonometric ratios (SOH CAH TOA):
   sin(45°) = \(\frac{\text{opposite}}{\text{hypotenuse}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}\)
   cos(45°) = \(\frac{\text{adjacent}}{\text{hypotenuse}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}\)
   tan(45°) = \(\frac{\text{opposite}}{\text{adjacent}} = \frac{1}{1} = 1\)
   

2. Using 30°-60°-90° Special Right Triangle:
   The sides of this triangle will be hypotenuse = 2, side opposite 30° = 1, and side opposite 60° = \(\sqrt{2^2 - 1^2} = \sqrt{3}\)
   Using the definitions of trigonometric ratios (SOH CAH TOA):
   sin(30°) = \(\frac{\text{opposite}}{\text{hypotenuse}} = \frac{1}{2}\)
   cos(30°) = \(\frac{\text{adjacent}}{\text{hypotenuse}} = \frac{\sqrt{3}}{2}\)
   tan(30°) = \(\frac{\text{opposite}}{\text{adjacent}} = \frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3}\)
   sin(60°) = \(\frac{\text{opposite}}{\text{hypotenuse}} = \frac{\sqrt{3}}{2}\)
   cos(60°) = \(\frac{\text{adjacent}}{\text{hypotenuse}} = \frac{1}{2}\)
   tan(60°) = \(\frac{\text{opposite}}{\text{adjacent}} = \frac{\sqrt{3}}{1} = \sqrt{3}\)
   

Trigonometric Function Values Of Special Angles

How to derive the trigonometric function values of 30, 45 and 60 degrees and their corresponding radian measure. Cofunction identities are also discussed:
sin θ = cos(90° - θ)
cos θ = sin(90° - θ)

• Show Video Lesson

How To Find Trig Ratios Of Special Angles?

This video shows how to find the trig ratios of the special angles: sine, cosine and tangent values of 0, 30, 45, 60 and 90 degrees. Scroll down the page for part 2.

• Show Video Lesson

How To Use The Trig Ratios Of Special Angles To Find Exact Values Of Expressions?

How to use the trig ratios of special angles to find exact values of expressions involving sine, cosine and tangent values of 0, 30, 45, 60 and 90 degrees?

Example:
Determine the exact values of each of the following:
a) sin30°tan45° + tan30°sin60°
b) cos30°sin45° + sin30°tan30°

• Show Video Lesson

How To Remember The Trig Ratios For Special Angles?

A Finger Trick for Trigonometry
If we insist that students memorize the values of sine and cosine for the basic angles 0, 30, 45, 60 and 90 degrees, then here’s a cute little trick for doing so using the fingers on your hand.

• Show Video Lesson

Cool Pattern For Trig Special Angles

A pattern to help you remember the Sine and Cosines of Special Angles in the first quadrant. 0, 30, 45, 60, 90 degrees.

• Show Video Lesson

How To Evaluate Trig Functions Of Special Angles?

Easy way to use right triangle and label sides to find sin, cos, tan, cot, csc, and sec of the special angles, and of angles at multiples of 90°. This is Part 1. Scroll down the page for part 2.

Example:
Find cos 90, tan 90, sin 630, sin 135, tan (-405), sin 210, tan (-30).

• Show Video Lesson

Trigonometric Functions Of Special Angles, Part 2

Example:
Find cos 300, cot 180, sin 1305, sec(-210), csc 750, cos 270, sin(-420).

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.