Surface Area Of A Cylinder
In these lessons, we will learn
- calculate the surface area of solid cylinders.
- calculate the surface area of hollow cylinders or tubes or pipes.
- solve word problems about cylinders.
- calculate the surface area of cylinders using nets.
Related Pages
Surface Area Formulas
Surface Area of Prisms
Surface Area of a Sphere
More Geometry Lessons
Surface Area of a Solid Cylinder
A cylinder is a solid that has two parallel faces which are congruent circles. These faces form the bases of the cylinder. The cylinder has one curved surface. The height of the cylinder is the perpendicular distance between the two bases.
The net of a solid cylinder consists of 2 circles and one rectangle. The curved surface opens up to form a rectangle.
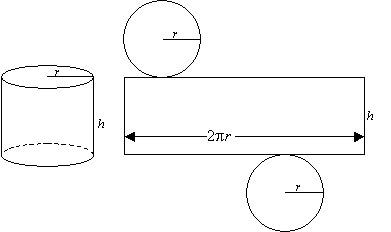
Surface area = 2 × area of circle + area of rectangle
Surface Area = 2πr2 + 2πrh = 2πr(r + h)
where r is the radius and h is the height.
Worksheets
Calculate the volume of cylinders
Calculate the surface area of cylinders
Volume and surface area of cylinders
Surface area of cylinders and pipes
Example:
The diameter of the base of a cylinder is 12 cm and the height is 8 cm. Find the surface area of the solid cylinder.
Solution:
Radius = 6 cm
Surface area = 2πr (r + h)
= ![]()
= 528 cm2
How to derive and use the formula of the surface area of a cylinder?
How to find the surface area of a cylinder?
Example:
Find the surface area of a cylinder with r = 18in, h = 17in.
How to calculate the surface area of a cylinder in terms of π?
Surface Area Of A Hollow Cylinder
Hollow cylinders like pipes or tubes have internal surfaces to consider.
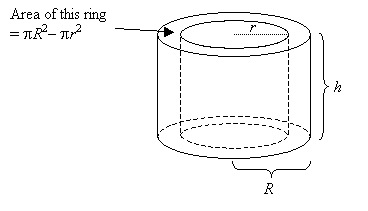
Total surface area of hollow cylinder
= area of internal curved surface + area of external curved surface + area of the two rings
![]()
Example:
The figure shows a section of a metal pipe. Given the internal radius of the pipe is 2 cm, the
external radius is 2.4 cm and the length of the pipe is 10 cm. Find the total surface area of the pipe.
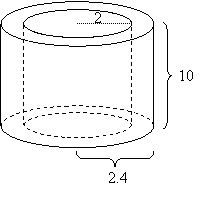
Solution:
r = 2, R = 2.4, h = 10
Total surface area of pipe
= area of internal surface + area of external surface + area of the two rings
= 2πrh + 2πRh + 2(πR2– πr2)
= (2π × 2 × 10) + (2π × 2.4 × 10) + (2 × (2.42π – 22π))
= 40π + 48π + 3.52π
= 91.52π
= 91.52 × 3.142
= 287.56 cm2
Word Problems Involving Cylinders
How many square feet of metal are used to make the can?
Find the surface area of a cylinder without the lid.
Surface Area Of Cylinder Using Nets
Use the net of a cylinder to determine its volume and surface area.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.