Surface Area of Cone
In these lessons, we will learn
- how to calculate the surface area of a cone when given the slant height.
- how to calculate the surface area of a cone when not given the slant height.
- how to solve word problems about cones.
- how to derive the formula for the surface area of a cone.
Related Pages
Surface Area Formula
Surface Area of Prisms
Surface Area of a Sphere
More Geometry Lessons
Geometry Worksheets
** Surface Area of a Cone**
A cone is a solid with a circular base. It has a curved surface which tapers (i.e. decreases in size) to a vertex at the top. The height of the cone is the perpendicular distance from the base to the vertex.
The net of a solid cone consists of a small circle and a sector of a larger circle. The arc of the sector has the same length as the circumference of the smaller circle.
The following figures show the formula for surface area of a cone. Scroll down the page if you need more examples and explanations.
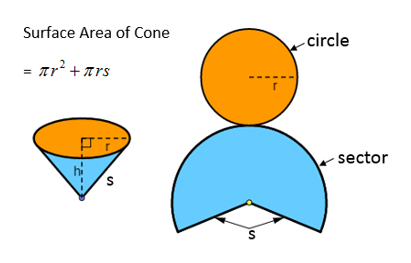
Surface area of cone = Area of sector + area of circle
= πrs + πr2
= πr(r + s)
Surface area of a cone when given the slant height
Example:
A cone has a circular base of radius 10 cm and a slant height of 30 cm. Calculate the surface area.
Solution:
Area = πr(r + s)
= 
= 1,257.14 cm2
How to find the surface area of a cone when the slant height is given?
Example:
Find the surface area. r = 9cm, h = 12cm, l = 15cm. (Leave answer in π form)
Example:
What is the surface area of the cone? Round the answer to the nearest hundredth.
Surface area of cone when not given the slant height
The following video shows how to find the surface area of a cone when not given the slant height.
Example:
Find the surface area. r = 7cm, h = 24cm. (Leave answer in π form)
How to calculate the surface area of a cone when the slant height is not given?
The Pythagorean Theorem will be used to calculate the slant height using the radius and height
of the cone as the right triangle’s legs.
Word Problems about cones
Example 1: A cone-shaped roof has a diameter of 12 ft. and a height of 8 ft. If roofing material comes in 120 square-foot rolls, how many rolls will be needed to cover this roof?
Example 2: The height of the Pyramid of Menkaure is 216 ft and the side of the (square) base measures 346 ft. Find the lateral surface area.
Derive the formula for the surface area of a cone
This video shows the derivation of the formula for the Surface Area of a Cone.
How to derive the formula for the surface area of a cone?
In this lesson, we’ll take a cone, slice it, squash it, dissect it, and figure out a
formula for its surface area.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.