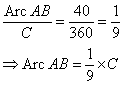SAT Practice Questions - Geometry
SAT Practice Questions for Geometry
These are some of the topics in Geometry that you will need to know for the New SAT Math Test (March 2016 and beyond).
Lines and Angles: Lengths and midpoints, Vertical angles, Straight angles and the sum of angles about a point, Properties of parallel lines and angles formed by a transversal, Properties of perpendicular lines.
Triangles and other polygons: Right triangles, Pythagorean Triples and the Pythagorean Theorem, Properties of equilateral and isosceles triangles, Properties of 30°-60°-90° triangles and 45°-45°-90° triangles, Congruent triangles and other congruent figures, Similar triangles and other similar figures, The triangle inequality, Quadrilaterals, Regular polygons.
Circles: Radius, diameter and circumference, Measure of central angles and inscribed angles, Arc Length and area of sectors, Tangents and chords.
Solids: Area, Surface Area and Volume.
New SAT Practice: Lines, Angles, Triangles
Examples:
- The area of triangle DEF is 32√3 square units. What is the length of DF?
- In the figure, what is the area of triangle QRS?
- If AD = 2CD, BD = BC = 6, what is the length of side AB?
- A triangle is graphed on a standard coordinate plane. What is the perimeter of the triangle if it has vertices (1,4), (1,7), and (4,4)?
- What is the area, in square units, of an isosceles right triangle with hypotenuse of 2?
New SAT Practice: Lines, Angles, Triangles (Hard)
Examples:
- Figure ABCD is a parallelogram. What is the product of xy?
- Each of the quadrilaterals is a square. The area of the smallest square, square 1, is 16 square units, the area of the medium square, square 2, is 48 square units. What is the area, in square units, of the largest square?
- Find the length of BC.
- Given that the sides of a right triangle are x, x - 2 and 2x - 2, what is the value of x?
New SAT Practice: Similarity, Congruence, Proofs (Easy)
Examples:
- Confirmation of which of the following facts would be sufficient to prove that the two triangles are congruent?
- While working on a geometry problem, Raul determines that the angles of one triangle are congruent to the corresponding angles of another triangle. Which of the following is a valid deduction that Raul can make?
A. The two triangles are congruent but not necessarily similar.
B. The two triangles are similar, but not necessarily congruent.
C. The two triangle are both similar and congruent.
D. The two triangles are neither similar nor congruent.
New SAT Practice: Similarity, Congruence, Proofs (Medium)
Examples:
-
AC and BD are diameters of circle E. Which triangle congruence theorem can be used to prove triangle AEB is congruent to triangle DEC?
-
If the right triangles are similar triangles, what is the length of the shorter leg of the larger triangle?
-
A triangle with side lengths 5, 12, 15 centimeters is similar to another triangle. The longest side of the other triangle has length 24 centimeters. What is the perimeter, in centimeters, of the larger triangle?
-
Two triangles are graphed on the coordinate plane. Triangle MNP has vertices M(-4,2), N(-4,6), P(-6,2). Triangle QRS has vertices Q(-5,-1), R(-5,-5), S(4,-5). Which of the following statements is true?
A. Triangle MNP is congruent to triangle QRS.
B. Triangle MNP is similar to triangle QRS.
C. Triangle MNP is similar to triangle RSQ.
D. The triangles are neither congruent nor similar. -
JK = KL, JL = 26. The ratio of MV to MP is 8:5. Find the length of JM?
New SAT Practice: Similarity, Congruence, Proofs (Hard)
Examples:
- Triangle CAT is an isosceles triangle with vertices (2,1), (6,1), (4,7). Triangle DOG is similar to CAT, and two of its vertices are (3,1) and (5,-1). If the third vertex has a y-coordinate that is less than -1, what are the coordinates of the third vertex?
- UY and WX are parallel. UX intersects WY at V. What is the length of WY?
- A scientist looking at a sample of infected tissue through a microscope wants to find the length x, in microns, across a damaged blood cell. The lengths represented by AB, EB, BD and CD are determined to be 26 microns, 22 microns, 11 microns, and 12 microns, respectively. Given that the measure of AEB is equal to the measure of CBD, what is the value of x?
The following materials relate to the SAT before March 2016.
For updated SAT materials, please see:
New SAT Prep
SAT Math
SAT Geometry
Try out the following Geometry Questions to help you prepare for the SAT, ACT or other similar examinations.
SAT Practice Questions - Geometry:
(Note: You may need to enable JavaScript on your browser for the hints and solutions to show properly.)
Question 6
John has a square piece of paper with sides 4 inches each. He rolled up the paper to form a cylinder. What is the volume of the cylinder?
(A) |
|
| (B) |  |
| (C) | 16 |
| (D) | 4π |
| (E) | 16π |
- Show Hint
-
Show Solution
Step 1: The edge of the paper will form the circumference of the base of
the cylinder.
Step 2: Volume of cylinder = area of base × height
Height = edge of the paper = 4
Answer: (B)
Question 7
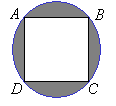
The square ABCD touches the circle at 4 points. The length of the side of the square is 2 cm. Find the area of the shaded region.
(A) |
π – 4 |
- Show Hint
-
Show Solution
Step 1: Area of shaded region = Area of circle – area of square.
We need to get the area of the circle and area of the square.
Step 2: The diagonal BD makes two 45°-45°-90° triangles with the sides of
the square.
Step 3: Using the 45°-45°-90° special triangle ratio. If the leg is 2
then the diagonal BD must be.
Step 4: BD is also the diameter of the circle.
Step 5: Area of square = 2 × 2 = 4
Step 6: Area of shaded region = Area of circle – area of square = 2π – 4Answer: (B) 2π – 4
. If the leg is 2 
. 
Question 8
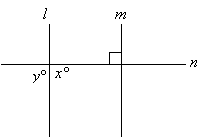
Note: Figures not drawn to scale
In the figure above, if x < 90° then which of the following must be true?
| (A) | l ∥ m |
| (B) | l ⊥ m |
| (C) | y < 90° |
| (D) | y = 90° |
| (E) | y > 90° |
- Show Hint
-
Show Solution
Step 1: x and y are supplementary angles. So if x < 90° then y > 90°
Beware! Although the figure seems to show that l is parallel to m, it is not
stated in the question.Answer: (E) y > 90°
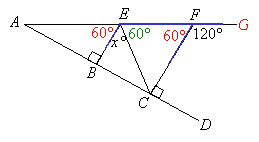
Question 9
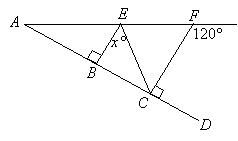
Note: Figures not drawn to scale
In the figure above, 
and 
and AE = EF . What is the value of x?
(A) |
40 |
- Show Hint
-
Show Solution
Step 1: We can find the supplementary angle of 120°, which gives us
60°.Step 2:
is parallel to because they are both perpendicular to . This means that since they are corresponding angles.Step 3: Triangle* ABE* and triangle* ACF* are similar triangles , since
and (AA rule). Given that *AE* = *EF*, we can conclude that *AB* = *BC*Step 4: Triangle* ABE* and triangle* CBE* are congruent triangles (SAS rule). So, *x* = angle AEB = 60°
So, x = 60
Answer: (E) 60
60°.
is parallel to 
because they are both perpendicular to 
. This means that 
since they are corresponding angles.
and 
(AA rule). Given that *AE* = *EF*, we can conclude that *AB* = *BC*Question 10
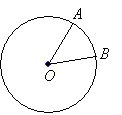
In the figure above, if ∠AOB = 40° and the length of arc AB is 4π, what is the area of the sector AOB?
(A) |
4π |
- Show Hint
-
Show Solution
Step 1: Arc AB = 40°. Circumference of circle = 360°
Let C = circumference of circle
Step 2: You are given that arc AB = 4π. Plug into above equation.
Step 3: Using the formula for the circumference of circle: C = 2πr. Plug into the above equation.
2πr = 36π
2r = 36
r = 18
Step 4: Using the formula for the area of circle: A = πr2. Plug in value for r.
A = π(18)2 = 324π
Step 5: Sector AOB is of the area of the circle.
Sector AOB = × 324π = 36πAnswer: (C) 36π
of the area of the circle.SAT Practice Questions - Geometry:
Example:
Which segment is congruent to BE?
Example:
Which line has a slope of -3?
Example:
AD is parallel to BC. AC = 13, BC = 5, BD = 15. What is the length of AD?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.