Reflection, Rotation and Translation

In geometry, transformations are operations that move or change a shape (called the pre-image) to create a new shape (called the image). Reflection, Rotation, and Translation are the three main types of rigid transformations (also known as isometries or congruence transformations). This means they preserve the size, shape, and angles of the original figure, only changing its position or orientation.

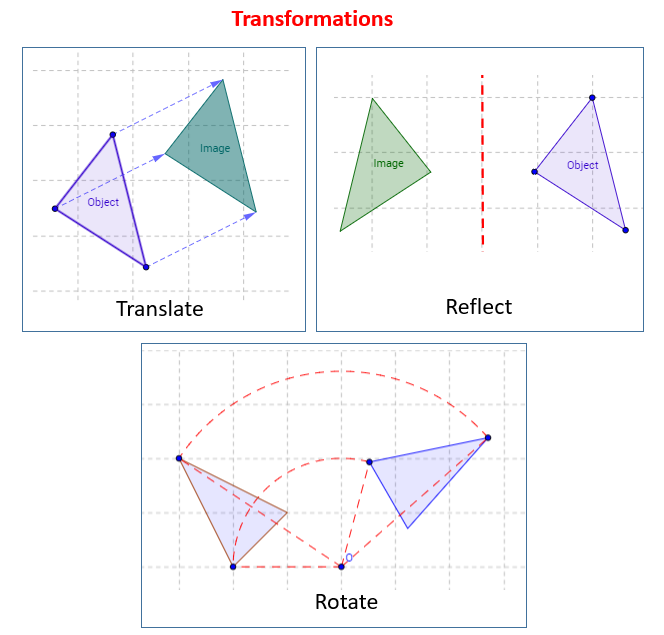
The following diagrams show the Transformations: Translation, Reflection and Rotation. Scroll down the page for examples and solutions.

 

Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Geometry Worksheets

Reflection (Flip)

A reflection is a transformation that flips a figure across a line, called the line of reflection, to create a mirror image. Each point in the original shape is mapped to a point that is the same distance from the reflection line but on the opposite side. Reflections preserve size and shape but reverse the orientation.

When reflecting a 2-D shape remember that:

• the shape and its image are of opposite orientation
• a 2-D shape and its image are congruent
• there is an equal distance from the mirror line to both the 2-D shape and its reflected image

When reflecting a 2-D shape across a horizontal line of reflection, the x-coordinates of the vertices do not change, but the y-coordinates do change.

When reflecting a 2-D shape across a vertical line of reflection, the y-coordinates of the vertices do not change, but the x-coordinates do change.

When reflecting a 2-D shape across a diagonal line of reflection, both the x-coordinates and y-coordinates of the vertices change.

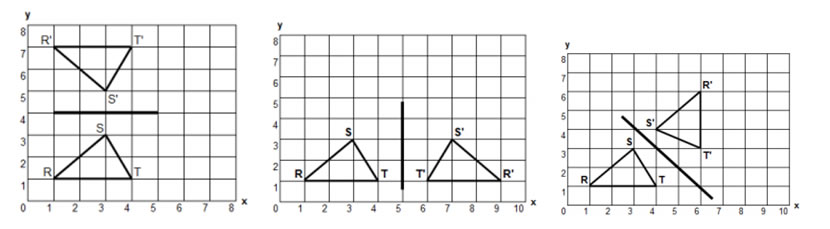
Transformations - Reflection

Rules for performing a reflection across an axis

1. When reflecting across the y-axis, the y-coordinates remain the same and the x-coordinates change to their opposites.
2. When reflecting across the y-axis, the x-coordinates remain the same and the y-coordinates change to their opposites.

• Show Video Lesson

Transformational Geometry - Reflection Over A Diagonal

In this video we perform a reflection of a shape over a diagonal line of reflection.
There are two examples, one where the shape overlaps the line of reflection.

• Show Video Lesson

Rotation (Turn)

A rotation is a transformation that turns a figure around a fixed point, called the center of rotation. Every point in the figure moves through the same angle, in the same direction (clockwise or counterclockwise), and maintains the same distance from the center of rotation. Rotations preserve size and shape but change the orientation.

When describing a rotation, we must include the amount of rotation, the direction of turn and the center of rotation.

Rotations can be described in terms of degrees (E.g., 90° turn and 180° turn) or fractions (E.g., 1/4 turn and 1/2 turn).

When describing the direction of rotation, we use the terms clockwise and counter clockwise.

In Grade 5, we rotated shapes about a vertex of that shape. In Grade 6, we will rotate about a centre of rotation on a vertex, outside the shape and within the shape.

When describing the positional change of the vertices of a given 2-D shape to the corresponding vertices of its image as a result of a rotation, remember that

• all vertices move together 1/4 (90°), 1/2 (180°) , or 3/4 (270°) of a turn in the same direction, either clockwise or counter clockwise
• the shape and its resulting image are congruent
• the orientation of the shape and its image are different

Using tracing paper we can trace the shape on the paper and place a dot on the point of rotation. Place the tip of a pencil on the point of rotation and turn tracing paper the indicated direction and amount for that particular rotation to see the position of the rotated image. We can then transfer the traced shape on the grid.

How To Rotate A Shape On A Coordinate Grid Using Tracing Paper?

In order to rotate a shape on a coordinate grid you will need to know the angle, the direction and the centre of rotation.

The angle could be 90 degrees (half turn), 180 degrees (1/2 turn) or 270 degrees ( ¾ turn). The direction can be clockwise or anticlockwise.

The centre of rotation is given as a coordinate and this is where you place your pencil on the tracing paper when you turn the shape around.

• Show Video Lesson

How to Performing a Rotation using Tracing Paper?

How to do a basic rotation using tracing paper.
This rotation used (0,0) as the rotation point and rotated 90° clockwise.

• Show Video Lesson

Translation (Slide)

A translation is a transformation that moves every point of a figure by the same distance in the same direction. It’s a “slide” without altering its size, shape, or orientation.

In a translation:

• the 2-D shape and its image are congruent
• the 2-D shape and its image have the same orientation (the vertices of the translated image will be in the same relative position as the original image).

Remember to label the vertices of the shape (e.g. A, B, C, D) and the corresponding vertices of the reflected image (A’, B’, C’, D’). A’ is read as A prime.

When describing the positional change of the vertices of a given 2 D shape to the corresponding vertices of its image as a result of a translation, we need to keep in mind the following:

• the shape and its image will have the same orientation
• all vertices move together
• each vertex moves the same way

If the translation is:

• to the left, the x- coordinate will decrease
• to the right, the x- coordinate will increase
• downward, the y- coordinate will decrease
• upward, the y- coordinate will increase

In the transformation shown below:
We describe the translation as " Left 4 and Up 3"
The x-coordinates of the vertices decreased by 4.
The y-coordinates of the vertices increased by 3.

Transformations - Translating A Triangle On The Coordinate Plane

This tutorial reviews how to perform a translation on the coordinate plane using a triangle.

• Show Video Lesson

Transformational Geometry (Translations, Rotations, Reflections)

• Show Video Lesson

Translation, Reflection, Dilation, and Rotation

• Show Video Lesson

Transformations

1. Reflections: transformation representing flip of a figure in a point, a line, or a plane.
2. Translation: transformation that moves all points of a figure the same distance in the same direction.

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.