Geometry - Grade 5 - Slide, Flip, Turn
Related Pages
More Geometry Lessons
Geometry Worksheets
Geometry Games
More Lessons for Grade 5 Math
Grade 5 Worksheets
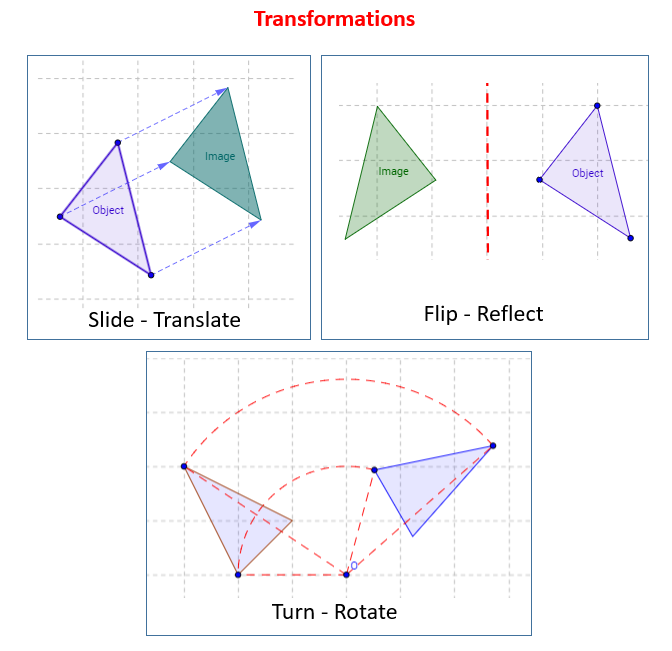
In these lessons, we will learn some transformations of 2D-shapes: translation (slide), reflection (flip) or rotation (turn).
The transformation of 2D shapes involves changing their position, size, or orientation on a 2D plane. There are four main types of transformations:
- Translation (Slide): This involves moving a shape from one location to another without changing its size, shape, or orientation. It’s like sliding the shape.
- Rotation (Turn): This involves turning a shape around a fixed point called the center of rotation. The shape’s size and shape remain the same, but its orientation changes. Rotation is defined by the angle of rotation (in degrees) and the direction (clockwise or counterclockwise).
- Reflection (Flip): This involves flipping a shape over a line called the line of reflection (or mirror line). The reflected image is a mirror image of the original shape, maintaining the same size and shape but with a reversed orientation.
- Dilation: This involves changing the size of a shape by a scale factor. The shape’s proportions remain the same, but it becomes either larger (enlargement) or smaller (reduction) depending on the scale factor. Dilation occurs with respect to a fixed point called the center of dilation.
In this lesson, we will learn about Translation (Slide), Rotation (Turn) and Reflection (Flip).
The following diagrams show the Transformations: Slide, Flip and Turn. Scroll down the page for more examples and solutions.
Transformation - Translation - Slide
In a translation or slide, a shape is moved along a straight line without turning. The shape in the new position is called a translation image of the shape. The translation is described by the number of squares moved right or left and up or down.
General properties to identify translations:
- the 2-D shape and its image are congruent
- the 2-D shape and its image have the same orientation (that is, if we go around the object ABCD in a clockwise direction, we should be able to also go around its image A’B’C’D’ in a clockwise direction.)
The translation rule for the following rectangle ABCD is 9 units right and 4 units up.
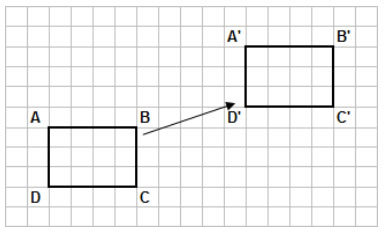
Translations - Slides
When a shape moves along a straight line without turning, it is translated from one position to another.
The movement is a translation or slide.
When we draw the shape in its new position, we draw a transition image of the shape.
The translation is described by the numbers of squares moved right or left and up or down.
A shape and its translation image have the same orientation; that is, they face the same way.
To transform a shape, you slide, flip, or turn it.
To translate a shape, you slide it over a line.
To reflect a shape, you flip it over a line.
To rotate a shape, you turn it around a point.
Translation of shapes
How to translate a shape?
Transformation - Reflection - Flip
A reflection is a flip over a the mirror line (line of reflection). The line of reflection is equal distance to both the 2-D shape and the reflected image. The line segment that joins a point to its image is perpendicular to the line of reflection.
A reflection can be identified if:
- a 2-D shape and its image are congruent
- a 2-D shape and its image are of opposite orientation (This is, if we go around the object ABCD in a clockwise direction, the image A’B’C’D’ would require a counter-clockwise direction.)
The following shape is reflected in a horizontal line of reflection.
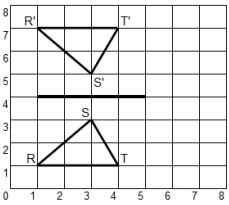
The following shape is reflected in a vertical line of reflection.
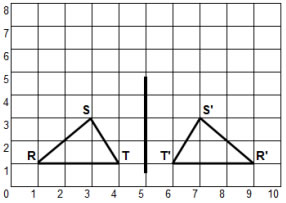
Reflections - Flips
Translations and Reflections
A video outlining the steps to translate (slide) and reflect (flip) shapes.
Translation:
Step 1: Choose one point to start at.
Step 2: Translate (slide) by counting the units from the start point.
Step 3: Choose another point to start at and repeat until finished.
Reflection:
Step 1: Choose one point to start at.
Step 2: Count the units to the Reflection Line.
Step 3: From the Reflection, count the same number of units away and place the point.
Step 4: Continue for each point until finished.
Transformation - Rotation - Turn
When a shape is turned around a fixed point, it is called rotation or turn. The shape may be turned clockwise or counterclockwise about the point. After one complete turn, the shape is back where it started.
The following diagram shows the rectangle ABCD rotated clockwise around the center C.
(Quarter turn, Half turn and Three-quarters turn)
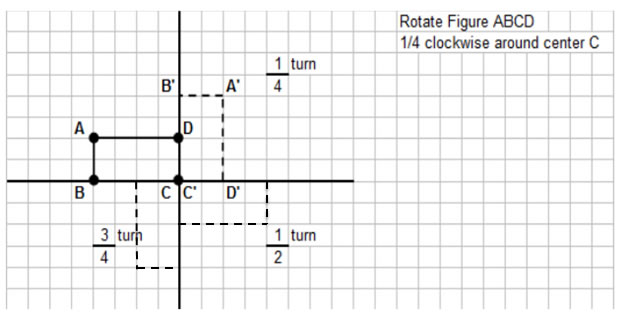
Rotations - Turns
A rotation is denoted by:
• the direction of the turn (clockwise or counterclockwise)
• the fraction of the turn, and
• the point of rotation
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.