Multiplying and Dividing Algebraic Expressions

Multiplying and dividing algebraic expressions are fundamental skills in algebra. These operations involve simplifying expressions by applying the distributive property, combining like terms, and following the rules of exponents.

Multiplying Algebraic Expressions

When multiplying algebraic expressions, use the distributive property and the rules of exponents. Using the distributive property, we can multiply two algebraic terms to get a product, which is also an algebraic term.

The following diagram shows how to multiply algebraic expressions. Scroll down the page for more examples and solutions on how to multiply expressions.

Steps for Multiplying Algebraic Expressions

1. Distribute Each Term:
   Multiply each term in the first expression by each term in the second expression.
   
2. Combine Like Terms:
   Simplify the expression by combining like terms.
   

Algebra Math Worksheets
Practice your skills with the following worksheets:
Printable & Online Algebra Worksheets

Example:
Evaluate 3pq³× 4qr

Solution:
3pq³× 4qr
= 3 × p × q × q × q × 4 × q × r
= 3 × 4 × p × q × q × q × q × r
= 12 × p × q⁴ × r
= 12pq⁴r

Example:
Evaluate –2a³b × 3ab²c

Solution:
–2a³b × 3ab²c
= –2 × 3× a³× a × b × b² × c
= –6 × a⁴ × b³ × c
= –6a⁴b³c

How to multiply algebraic terms or variables?

1. Multiply the numbers (coefficients)
2. Multiply the variables - exponents can be combined if the base is the same.

Examples:

1. 3a²(-5a⁴)
2. -2c²(-7c³x⁵)(bx²)²
3. 3a³(-ab⁴)(2a²c³)

How to multiply algebraic expressions?
Using the distributive law to multiply algebraic expressions:

1. 3sy(s - t)
2. 4uv²(3²z - 7u³)

• Show Video Lesson

How to multiply expressions using the distributive law?
Solve the following questions

1. 3cy²(-4cx - 2xy³)
2. (x + 5)(x - 2)

• Show Video Lesson

Multiplication of Algebraic Expressions - Solving Complex Questions

Examples:

1. (b + 3c)²
2. (2y - 4)³

• Show Video Lesson

Dividing Algebraic Expressions

Dividing algebraic expressions involves simplifying fractions where the numerator and/or denominator are polynomials. The key steps include factoring, canceling common factors, and using polynomial long division when necessary.

The following diagram shows how to divide algebraic expressions. Scroll down the page for more examples and solutions on how to divide expressions.

How to divide algebraic terms or variables?
We can divide an algebraic term by another algebraic term to get the quotient. The steps below show how the division is carried out.
Step 1: Write the division of the algebraic terms as a fraction.
Step 2: Simplify the coefficient.
Step 3: Cancel variables of the same type in the numerator and denominator.

How to divide Algebraic Expressions?
Step 1: Factor both the numerator and the denominator completely.
Step 2: Cancel out any common factors in the numerator and denominator.
Step 3: Write the simplified expression.

When dividing, be mindful that the denominators cannot be zero.

Example:
Evaluate 6pq³ ÷ 3pq

Solution:

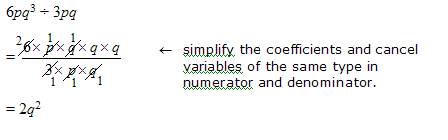
Example:
Evaluate –8a³bc ÷ 2ab

Solution:

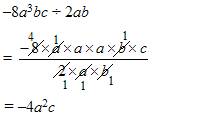
How to divide algebraic terms or variables?
Examples:

1. -8x⁵ ÷ - 5x³
   
2. -4x³ ÷ 7x⁹

• Show Video Lesson

Multiplying & Dividing Algebraic Fractions
Examples of dividing variables and dividing polynomials

• Show Video Lesson

Algebra - Division of Algebraic Expressions - Solving Questions.

• Show Video Lesson

Algebra - Division of Algebraic Expressions - Practice Questions.

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.