Midpoint Formula

In this lesson, we will learn

• the midpoint formula. Click here
• how to find the midpoint given two endpoints. Click here
• how to find one endpoint given the midpoint and another endpoint. Click here
• how to proof the midpoint formula. Click here

We have included a midpoint calculator at the end of this lesson.

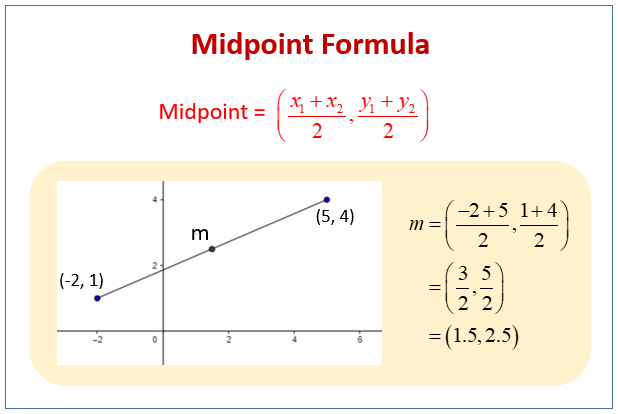
The Midpoint Formula

Some coordinate geometry questions may require you to find the midpoint of line segments in the coordinate plane. To find a point that is halfway between two given points, get the average of the x-values and the average of the y-values.

The following diagram shows the midpoints formula for the two points (x₁,y₁) and (x₂,y₂). Scroll down the page for more examples and solutions on how to use the midpoint formula.

For Example:
The midpoint of the points A(1,4) and B(5,6) is

Find the midpoint given two endpoints

We can use the midpoint formula to find the midpoint when given two endpoints.

Example:
Find the midpoint of the two points A(1, -3) and B(4, 5).

Solution:
Midpoint = = (2.5, 1)

Midpoint Worksheet 1
Midpoint Worksheet 2 to calculate the midpoint.

How to use the formula for finding the midpoint of two points?

Example:
Find the midpoint of the two points (5, 8) and (-5, -6).

• Show Video Lesson

How to use the midpoint formula given coordinates in fractions?

Example:
Determine the midpoint of the two points (2/3, 1/4) and (11/6, 7/9).

• Show Video Lesson

Find an endpoint when given a midpoint and another endpoint

We can use the midpoint formula to find an endpoint when given a midpoint and another endpoint.

Example:
M(3, 8) is the midpoint of the line AB. A has the coordinates (-2, 3), Find the coordinates of B.

Solution:
Let the coordinates of B be (x, y)

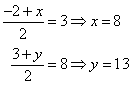
Coordinates of B = (8, 13)

How to find a missing endpoint when given the midpoint and another endpoint?

How to solve problems using the Midpoint Formula?

Example:
For a line segment DE, one endpoint is D(6, 5) and the midpoint M(4, 2). Find the coordinates of the other endpoint, E.

• Show Video Lesson

Proof of the Midpoint Formula

How to derive the midpoint formula by finding the midpoint of a line segment?

• Show Video Lesson

How to use the Pythagorean theorem to prove the midpoint formula?
The following video gives a proof of the midpoint formula using the Pythagorean Theorem.
Step 1: Use the distance formula to show the midpoint creates two congruent segments.
Step 2: Use the slope formula to show that the coordinate of the midpoint is located on the line segment.

• Show Video Lesson

Midpoint Calculator
Enter the coordinates of two points and the midpoint calculator will give the midpoint of the two points. Use this to check your answers.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.