Linear Programming
In these lessons, we will learn about linear programming and how to use linear programming to solve word problems.
Related Pages
Linear Programming
Graphing Linear Inequalities
Systems of Linear Inequalities
Many problems in real life are concerned with obtaining the best result within given constraints. In the business world, people would like to maximize profits and minimize loss; in production, people are interested in maximizing productivity and minimizing cost. However, there are constraints like the budget, number of workers, production capacity, space, etc. Linear programming deals with this type of problems using inequalities and graphical solution method.
Example:
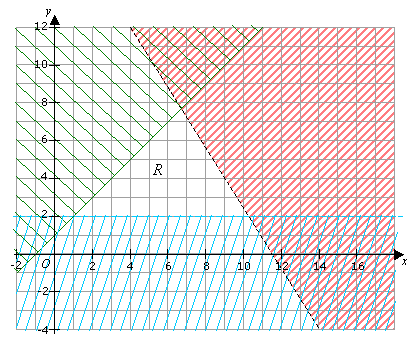
On the graph below, R is the region of feasible solutions defined by inequalities y > 2, y = x + 1
and 5y + 8x < 92. Find the greatest value of 2y + x which satisfies the set of inequalities,
where x and y are integers.
Solution:
We are looking for integer values of x and y in the region R where 2y + x has the greatest
value. We could substitute all the possible (x , y) values in R into 2y + x to get the largest value
but that would be too long and tedious.
A better method would be to find the line 2y + x = c where x and y are in R and c has the largest possible value. In this case, the equation 2y + x = c is known as the linear objective function.
Rewriting 2y + x = c as y = – 
x + c, we find that the gradient of the line is –
.
We need to find a line with gradient – 
, within the region R that has the greatest value for c.
Draw a line on the graph with gradient – . (Any line with a gradient of – would be acceptable).
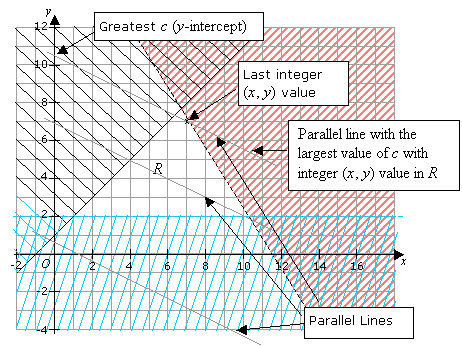
To look for the line, within R , with gradient – and the greatest value for c, we need to find the line parallel to
the line drawn above that has the greatest value for c (the y-intercept). We can use the technique in the
previous section to construct parallel lines. We will draw parallel lines with increasing values of c.
(Increasing values of c means we move upwards). We will stop at the parallel line with the largest c that
has the last integer value of (x , y) in the region R.
Solving Linear Programming Problems
Now, we have all the steps that we need for solving linear programming problems, which are:
Step 1: Interpret the given situations or constraints into inequalities.
Step 2: Plot the inequalities graphically and identify the feasible region.
Step 3: Determine the gradient for the line representing the solution (the linear objective function).
Step 4: Construct parallel lines within the feasible region to find the solution.
Example:
Joanne wants to buy x oranges and y peaches from the store. She must buy at least 5 oranges and the number of
oranges must be less than twice the number of peaches. An orange weighs 150 grams and a peach weighs 100 grams.
Joanne can carry not more than 3.6 kg of fruits home.
a) Write 3 inequalities to represent the information given above.
b) Plot the inequalities on the Cartesian grid and show the region that satisfies all the inequalities.
Label the region S.
c) Oranges cost $0.70 each and peaches cost $0.90 each. Find the maximum that Joanne can spend buying the fruits.
Solution:
a) at least 5 oranges: x ≥ 5
oranges less than twice of peaches: x < 2y
not more than 3.6 kg: 150x + 100y ≤ 3600 ⇒ 3x + 2y ≤ 72
b) Write out the equations for the inequalities and draw them on the graph paper. Choose the scales
so that the feasible region is shown fully within the grid. (if necessary, draft it out on a graph paper first.)
Shade out all the unwanted regions and label the required region S
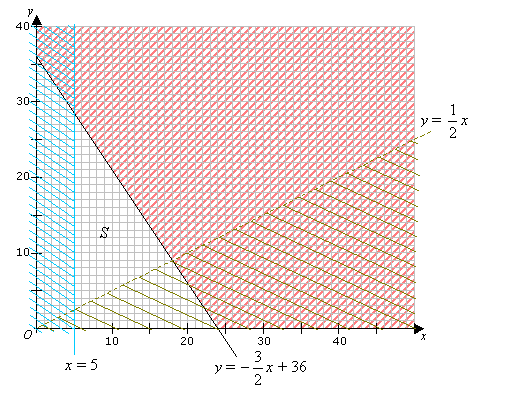
c) We need to find the maximum that Joanne can spend buying the fruits. This would mean looking for the
maximum value of c for 70x + 90y = c .
70x + 90y = c
y = 
We need to find the line with gradient 
with maximum value of c such that (x, y) is in the region S.
Plot a line and with gradient move it to find the maximum within the region S. Draw parallel lines with increasing
values of c. (Increasing values of c means we move upwards). Stop at the parallel line with the largest
c that has the last integer value of (x , y) in the region S.
The maximum value is found at (5,28) i.e. 5 oranges and 28 peaches. Therefore, the maximum that Joanne can spend on the fruits is: 70 × 5 + 90 × 28 = 2870 cents = $28.70.
It also possible to test the vertices of the feasible region to find the minimum or maximum values, instead of using the linear objective function. The following videos gives examples of linear programming problems and how to test the vertices.
Linear Programming Example:
Maximize C = x + y given the constraints,
y ≥ 0
x ≥ 0
4x + 2y ≤ 8
2x − y ≤ 0
Solving for Maxima-Minima
Maximize C = x + y given the constraints,
− 3x + 2y ≤ 6
3x + y ≤ 3
y ≥ 0
Linear Programming Steps and Example
- Graph the inequalities and find the vertices.
- Compute the function at the vertices. Largest = Max, Smallest = Min.
Problem:
Constraints are
240 acres of land.
Profit $40/acre corn, $30/acre oats.
Have 320 hrs available. Corn takes 2 hrs of labor per acre, oats requires 1 hr.
How many acres of each should be planted to maximize profits?
How to solve a word problem using linear programming?
First, find the equation that needs to be maximized or minimized as well as create the corresponding inequalities and then solve.
Example:
A rancher is mixing two types of food, Brand X and Brand Y, for his cattle. If each serving is
required to have 60 grams of protein and 30 grams of fat, where Brand X has 15 grams of protein
and 10 grams of fat and costs 80 cents per unit, and Brand Y contains 20 grams of protein
and 5 grams of fat and costs 50 cents per unit, how much of each type should be used to
minimize cost to the rancher?
Linear Programming Word Problem
Example:
A refinery produces both gasoline and fuel oil, and sells gasoline for $1 per gallon and fuel oil for
$0.90 per gallon. The refinery can produce at most 600,000 gallons a day, but must produce at least
two gallons of fuel oil for every gallon of gasoline. At least 150,000 gallons of fuel oil must be
produce each day to meet current demands. How much of each type of fuel should be produced to
maximize daily profits?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.