

Systems of Linear Inequalities
More Lessons for Algebra
Math Worksheets
We can solve systems of linear inequalities either algebraically or graphically.
Solving Systems of Linear Inequalities Algebraically
When solving systems of linear inequalities (or simultaneous inequalities):
Step 1: Solve each inequality separately
Step 2: Find the common values between the two inequalities. (Use a number line if necessary)
Example:
Solve the following simultaneous inequalities and represent your solution set on the number line.x + 2 < 6 and x – 3 > – 1
Solution:
x + 2 < 6
x < 6 – 2
x < 4
x – 3 > – 1
x > – 1 + 3
x > 2
Common values: 2 < x < 4
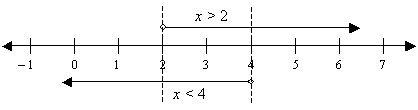
Example:
Find the integer values of x satisfying the simultaneous inequality:
6 < 2 – 3x < 14
Solution:
Write 6 < 2 – 3x < 14 as two separate inequalities and solve them separately.
6 < 2 – 3x
3x < 2 – 6
3x < – 4
x < ![]()
2 – 3x < 14
– 3x < 14 – 2
– 3x < 12
3x > –12
x > – 4
Common values: – 4 < x < ![]()
The integer values of x are –3 and –2
Solving System of Linear Inequalities Graphically
We can also solve systems of linear inequalities graphically. The following videos show some examples of solving systems of linear inequalities graphically
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.