Function Transformation

General Form:
A transformed function can be represented in the general form:
y = af(b(x - h)) + k
Where:
f(x) is the original function (the “parent function”).
a, b, h, and k are constants that determine the transformations.

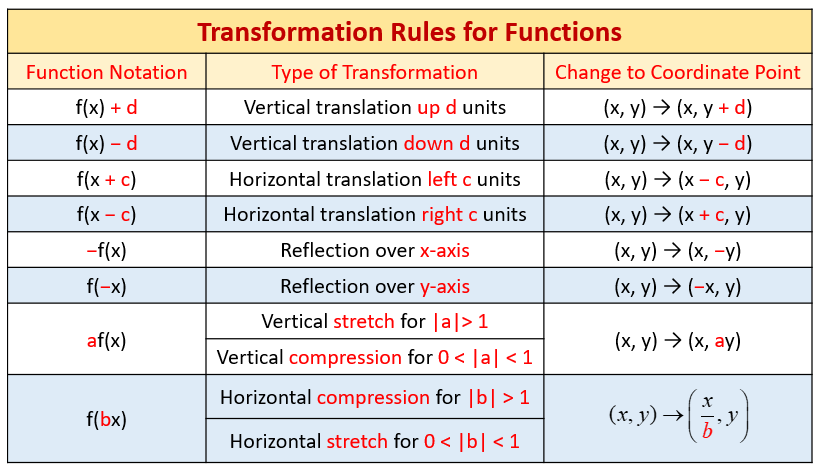
The following table gives the transformation rules for functions: Vertical and horizontal translations, Reflection over the x-axis and y-axis, Vertical and horizontal stretch, Vertical and horizontal compression. Scroll down the page for examples and solutions on how to use the transformation rules.

Functions Transformations: A Summary

This video reviews function transformation including stretches, compressions, shifts left, shifts right, and reflections across the x and y axes. Scroll down the page for more explanations and videos.

• Show Video Lesson

Types of Transformations:

1. Vertical Shifts (Translations):
   y = f(x) + k: Shifts the graph up by k units if k > 0, and down by |k| units if k < 0.
   Example: y = x² + 3 shifts the parabola y = x² up by 3 units.
   Example: y = x² - 2 shifts the parabola y = x² down by 2 units.
   

2. Horizontal Shifts (Translations):
   y = f(x - h): Shifts the graph right by h units if h > 0, and left by |h| units if h < 0. Note the minus sign in the formula.
   Example: y = (x - 4)² shifts the parabola y = x² right by 4 units.
   Example: y = (x + 1)² shifts the parabola y = x² left by 1 unit (because x + 1 can be rewritten as x - (-1)).
   

3. Vertical Stretches/Compressions (Dilations):
   y = a f(x):
   If |a| > 1: Stretches the graph vertically by a factor of |a|. The graph becomes “taller."
   If 0 < |a| < 1: Compresses the graph vertically by a factor of |a|. The graph becomes “shorter."
   If a < 0: Also reflects the graph across the x-axis (see reflections below).
   Example: y = 2x² stretches the parabola y = x² vertically by a factor of 2.
   Example: y = (1/2)x² compresses the parabola y = x² vertically by a factor of 1/2.
   

4. Horizontal Stretches/Compressions (Dilations):
   y = f(bx):
   If |b| > 1: Compresses the graph horizontally by a factor of |b|. The graph becomes “narrower."
   If 0 < |b| < 1: Stretches the graph horizontally by a factor of 1/|b|. The graph becomes “wider."
   If b < 0: Also reflects the graph across the y-axis (see reflections below).
   Example: y = (2x)² compresses the parabola y = x² horizontally by a factor of 2.
   Example: y = (1/3x)² stretches the parabola y = x² horizontally by a factor of 3.
   

5. Reflections:
   Reflection across the x-axis: y = -f(x). This flips the graph over the x-axis.
   Example: y = -x² reflects the parabola y = x² over the x-axis, making it open downwards.
   Reflection across the y-axis: y = f(-x). This flips the graph over the y-axis.
   Example: y = √(-x) reflects the square root function y = √x over the y-axis.
   

6. Order of Transformations:
   When multiple transformations are applied, the order matters. Generally, follow this order (similar to the order of operations):
   

• Horizontal shifts (h)
  
• Horizontal stretches/compressions and reflections (b)
  
• Vertical stretches/compressions and reflections (a)
  
• Vertical shifts (k)

Function Transformations: Horizontal And Vertical Stretches And Compressions

This video explains to graph graph horizontal and vertical stretches and compressions in the form a*f(b(x-c))+d. This video looks at how a and b affect the graph of f(x).

af(x): a > 1, stretch f(x) vertically by a factor of a
af(x): 0 < a < 1, compress f(x) vertically by a factor of a
f(bx); b > 1, compress f(x) horizontally
f(bx); 0 < b < 1, stretch f(x) horizontally.

• Show Video Lesson

Function Transformations: Horizontal And Vertical Translations

This video explains to graph graph horizontal and vertical translation in the form af(b(x-c))+d. This video looks at how c and d affect the graph of f(x).

f(x + c): shift f(x) c units left
f(x − c): shift f(x) c units right
f(x) + d: shift f(x) d units up
f(x) − d: shift f(x) d units down

• Show Video Lesson

Identify Function Translations Using Function Notation

This video explains how to identify a shift up, down, left, and right given the translation in function notation.

• Show Video Lesson

Graphing Multiple Function Transformations - Part 1 of 2

• Show Video Lesson

Graphing Multiple Function Transformations - Part 2 of 2

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.