Exterior Angle Theorem
In these lesson, we will learn
- the Exterior Angle Theorem
- how to use the Exterior Angle Theorem to solve problems
- how to prove the Exterior Angle Theorem
Related Pages
Exterior Angles Of A Triangle
Types Of Triangles
Interior Angles of a Triangle
Angles In A Triangle
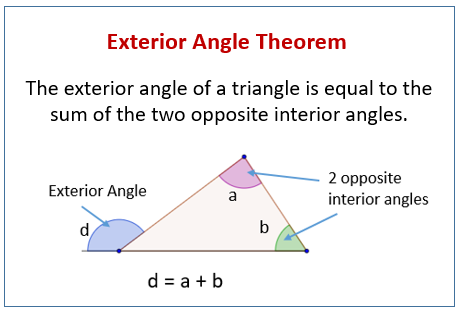
Exterior Angle Theorem
An exterior angle of a triangle is formed by any side of a triangle and the extension of its adjacent side.
The Exterior Angle Theorem states that:
An exterior angle of a triangle is equal to the sum of the two opposite
interior angles.
The following diagram shows the exterior angle theorem. Scroll down the page for more examples and solutions using the exterior angle theorem to solve problems.
Using The Exterior Angle Theorem To Solve Problems
Example:
Find the values of x and y in the following triangle.
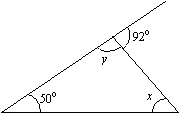
Solution:
x + 50° = 92° (sum of opposite interior angles = exterior angle)
x = 92° – 50° = 42°
y + 92° = 180° (interior angle + adjacent exterior angle = 180°.)
y = 180° – 92° = 88°
What is the Exterior Angle Theorem and how it can be used the find the angles in a triangle?
An exterior angle of a triangle is formed when an side is extended outwards
The exterior angle theorem states that the exterior angle of a triangle is equal to the sum of the opposite interior angles.
We can derive the exterior angle theorem using the information that
- The angles on a straight line add up to 180°
- The interior angles of a triangle add up to 180°
The exterior angle theorem of geometry
The exterior angle theorem is used to work out some applications in finding angles of a triangle.
Exterior Angle Theorem
This video discusses the exterior angle theorem. It also defines what exterior and remote interior angles are.
It solves two example problems in detail. The first example problem is pretty basic. The second example problem
is much harder.
An exterior angle is an angle formed by the extension of one side of a triangle.
The remote interior angles are the two interior angles of the triangle not adjacent to the exterior angle.
Example:
Identify the exterior angle and the remote interior angles in each problem, then solve for the missing angle.
How to use the Exterior Angle Theorem to solve problems involving angles in a triangle?
Proof Of The Exterior Angles Theorem
This video provides a two column proof of the exterior angles theorem
External Angle Theorem - Proof and Examples
This video proves the “External Angle Theorem” (sometimes called the External Angle Conjecture), and then
works some typical example problems where this concept might be applied.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.