Secant, Cosecant and Cotangent
In these lessons we will look at the reciprocal trigonometric functions: secant, cosecant and cotangent.
Related Pages
Trigonometric Functions
Trigonometric Graphs
Lessons On Trigonometry
Trigonometric Identities
We can get three more trigonometric functions by taking the reciprocals of three basic functions: sine, cosine and tangent.
The secant function is the reciprocal of the cosine function. The abbreviation of secant is sec.
The cosecant function is the reciprocal of the sine function. The abbreviation of cosecant is csc or cosec.
The cotangent function is the reciprocal of the tangent function. The abbreviation of cotangent is cot.
The following diagram shows the Reciprocal Trigonometric Functions. Scroll down the page for more examples and solutions on how to use the reciprocal trigonometric functions.
Example:
Given that 
, and that θ is acute, find, without using a calculator, the value of
a) sec θ
b) cot θ
Solution:
We can use the Pythagorean theorem to get the third side of the right triangle.
a) We then get that
b) We have
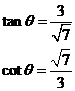
Videos
Reciprocal Ratios: Cosecant, Secant, Cotangent.
Opposite Sides, Adjacent Sides and Hypotenuse of a Right Triangle
Definition of Cos, Sin, Tan, Csc, Sec, Cot
Find the Cosecant of an Angle in a Right Triangle
Given any two sides of a right triangle, you can find any of the 6 trigonometric ratios. This problem demonstrates how to determine the cosecant of a right triangle. Using the Pythagorean Theorem to find a missing side is demonstrated.
Reciprocal Identities of Trig Functions
This tutorial covers the reciprocal identities and shows them in various forms.
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.