Area Formulas
In these lessons, we have compiled
- a table of area formulas and perimeter formulas used to calculate the area and perimeter of two-dimensional geometrical shapes: square, rectangle, parallelogram, trapezoid (trapezium), triangle, rhombus, kite, regular polygon, circle, and ellipse.
- a more detailed explanation (in text and video) of each area formula.
Related Pages
Area Of Triangles
Area Of Polygons
Area Of Circles
More Geometry Lessons
The following table gives the formulas for the area and perimeter of square, rectangle. parallelogram, trapezoid (trapezium), triangle, rhombus, kite, regular polygon, circle, and ellipse. Scroll down the page if you want more examples and explanations for the areas and perimeters.
Area of a Square
The area of a square is equal to the length of one side squared.
Area of a square = s2
How to find the area of a square?
The formula for the area of a square is s × s = s2, where s is the length of a side of the square.
Area of Rectangle
A rectangle is a 4-sided polygon where all four of its angles are right angles. Normally, the longer side is called the length and the shorter side is called the width. If all the sides are of equal length then it will be called a square.
Area of rectangle = length × width
A = lw
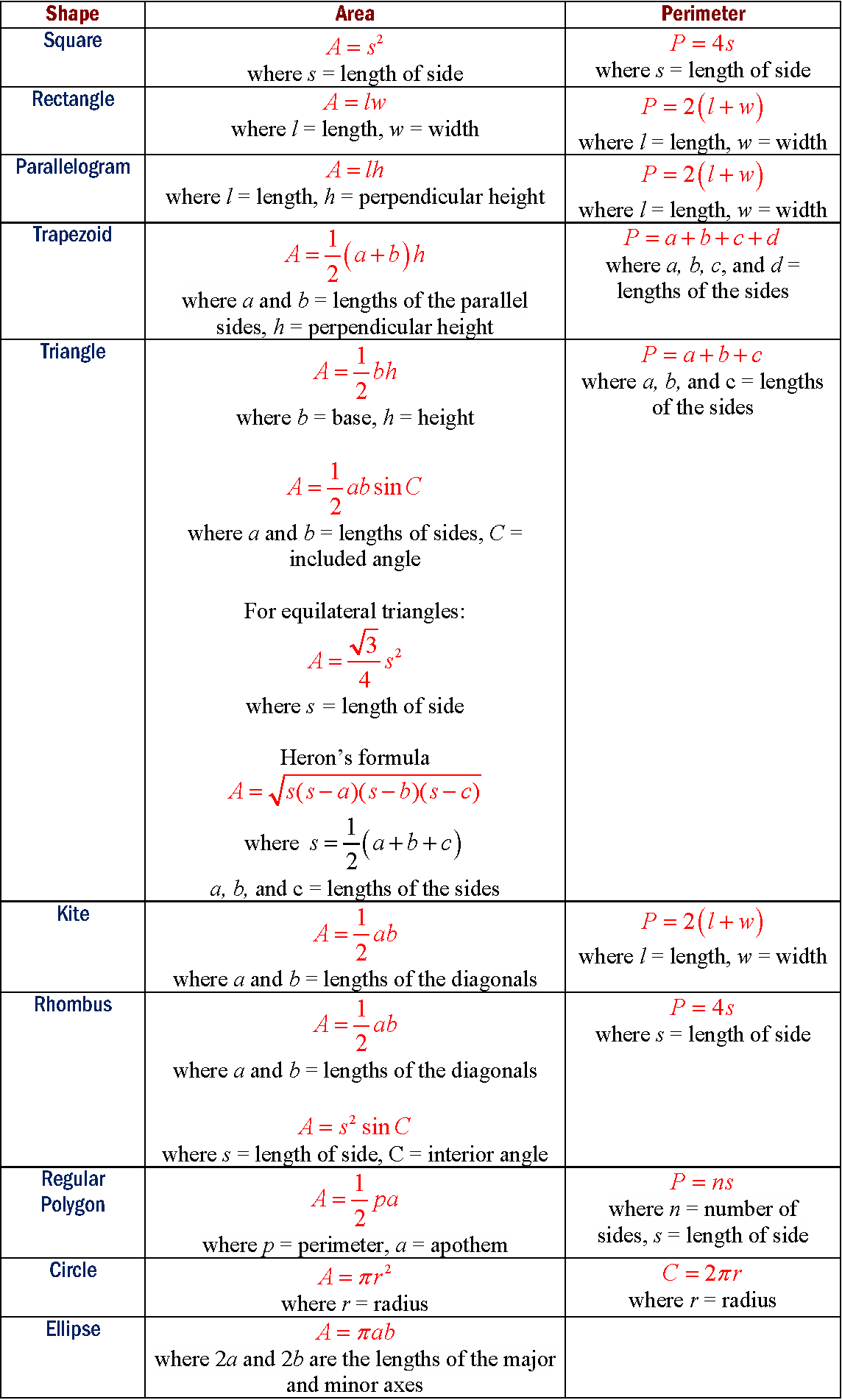
Area of Parallelogram
A parallelogram is a 4-sided polygon that has two sets of parallel sides. The opposite sides of a parallelogram are of equal length and the opposites angles are equal.
Area of parallelogram = base × perpendicular height
A = bh
How to find the area of a rectangle, triangle and parallelogram, using base and height?
Always use the height that is perpendicular to the base. Do not use the slant height.
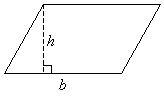
Area of Trapezoid / Trapezium
A trapezoid or trapezium is a 4-sided polygon that has at least one pair of parallel side. It is called a trapezoid in North America and a trapezium in Britain and other countries.
Area of trapezium = 
× (sum of two parallel sides) × height
A = × (a + b) × h
How to find the area of a trapezoid?
Remember to use the height that is perpendicular to the base.
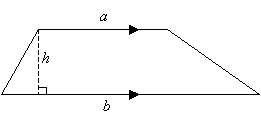
Area of Triangle (given base and height)
A triangle is a 3-sided polygon.
Area of triangle = × Base × Height
A = bh
How to use the formula of half the product of the base and height to calculate the area of a triangle?
Area of Triangle (given 2 sides and an included angle)
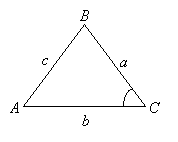
Area of triangle = ab sin C
How to find the area of a triangle given side-angle-side (SAS)?
We can find the area of the triangle using a formula that uses the sine function.
Area of Triangle (given 3 sides)
Area of triangle = 
This is also called the Heron’s Formula
How to find the area of a triangle given the 3 sides?
The following video shows how to use the Heron’s Formula.
Area of an Equilateral Triangle
To find the area of an equilateral triangle, we can use the following formula:
The area of an equilateral triangle (with all sides congruent) is equal to
where s is the length of any side of the triangle
What is the formula for the area of an equilateral triangle given the length of its side?
Given side of length s, the area of an equilateral triangle is s-squared times the square root of three over four.
Area of Rhombus (given the length of the diagonals)
A rhombus is a 4-sided polygon that has 4 equal sides. The diagonals of a rhombus bisects each other at right angles.
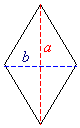
Area of rhombus = 
product of diagonals
Area of Rhombus (given length of side and an angle)
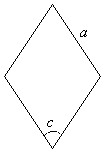
Area of rhombus = a2 sin c where a is the length of the side and c is any interior angle.
(You can use any interior angle because either they are equal or they are supplementary and supplementary angles have the same sine.)
How to find the area of a rhombus given a diagonal and two angles?
Example:
What is the area of a rhombus that has two 120 degrees angle and a longer diagonal measuring 10 meters?
Area of Kite (given the length of the diagonals)
A kite is a 4-sided polygon that has two distinct pairs of adjacent sides that are congruent. The diagonals of a kite bisects each other at right angles.
Area of a kite uses the same formula as the area of a rhombus
Area of kite = product of diagonals
Area of Regular Polygon
A regular polygon is a polygon where all the sides are the same length and all the angles are equal.
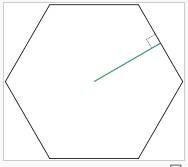
The apothem of a regular polygon is a line segment from the centre of the polygon to the midpoint of one of its sides.
Area of regular polygon = 
where p is the perimeter and a is the apothem.
How to find the area of a regular polygon, given the apothem and the length of the side?
Area of Circle
A circles is a shape consisting of those points in a plane which are at a constant distance, called the radius, from a fixed point, called the center.
Area of circle = π × (radius)2
A = πr2
How to find the area of a circle given the radius or diameter?
Area of Sector
A sector is the portion of circle that is enclosed by two radii and an arc.
How to calculate the area of a sector in degrees?
Area of Ellipse
An ellipse is a curved line forming a closed loop, where the sum of the distances from two points (foci) to every point on the line is constant. It looks like a circle that has bee squashed into an oval.
If 2a and 2b are the lengths of the major and minor axes of the ellipse, then the area of the ellipse is πab.
How to find the area of an ellipse given the lengths of the major axis and minor axis?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.