Area of Polygons
Related Topics:
High School Geometry
Worksheets, and activities to help Geometry students.
In these lessons, we will learn
- how to calculate the area of kites and rhombuses
- how to define the apothem and center of a polygon
- how to find the area of a regular polygon
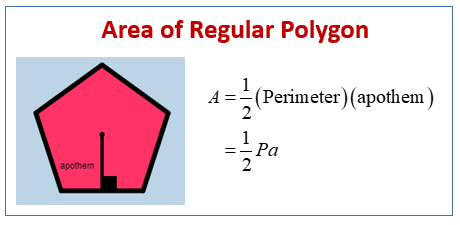
The following diagram gives the formula to find the area of a regular polygon using the perimeter and the apothem. Scroll down the page for more examples and solutions.
Area of Kites and Rhombuses
The area formula for a kite is found by rearranging the pieces formed by the diagonals into a rectangle. Since one side is half of a diagonal, the area of a rhombus formula is one half the product of the diagonals. An additional formula for the area of a rhombus is to use the kite formula (it works because rhombuses are technically kites). Related topics include area of parallelograms and solving formulas.
How to derive the area formula of a kite based on the rectangle formula; how to calculate the area of a rectangle using diagonal lengths.
This video investigates how to determine the area of a kite/rhombus using a kite formula.
Center and Apothem of Regular Polygons
An apothem is a perpendicular segment from the center of a regular polygon to one of the sides. When radii are drawn from the center to the vertices of the polygon, congruent isosceles triangles are formed with the polygon apothem as the height. These triangles are used in calculating the area of regular polygons. Related topics include properties of isosceles triangles and area of triangles.
How to define the apothem and center of a polygon; how to divide a regular polygon into congruent triangles. This lesson gives a detailed view of regular polygons. In addition to identifying terms associated with regular polygons, a few examples regarding area are discussed.
Finding the area of regular polygons.
This video
- discusses the parts of a regular polygon: apothem and radius.
- models how to find the different angles of a regular polygon formed by the radius and the apothem.
- discusses the formula to find the area of a regular polygon.
- gives two examples of finding the area of regular polygons are modeled.
Area of Regular Polygons
If radii are drawn from the center of a regular polygon to the vertices, congruent isosceles triangles are formed. Using the apothem as the height and the polygon side as the base, the area of each triangle can be calculated and summed. Therefore, the area regular polygons is equal to the number of triangles formed by the radii times their height: (side length)(apothem length)(number of sides)/2.
How to derive the formula to calculate the area of a regular polygon.
This video shows you how to use a formula to find the area of any regular polygon.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.