Antiderivative

Definition of Antiderivative

A function F is called an antiderivative of f on an interval I if F’(x) = f(x) for all x in I.

Formula for the antiderivatives of powers of x

The general antiderivative of f(x) = xⁿ is

where c is an arbitrary constant.

Example:

Find the most general derivative of the function f(x) = x^–3

Solution:

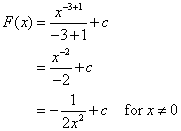
Formulas for the antiderivatives of trigonometric functions

Example:

Find antiderivative of the function

Solution:

Rewrite the given function as follows:

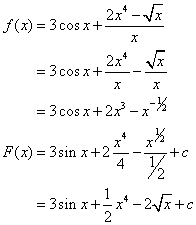
Videos

Definition of Antiderivatives
Antiderivatives are the opposite of derivatives. An antiderivative is a function that reverses what the derivative does. One function has many antiderivatives, but they all take the form of a function plus an arbitrary constant. Antiderivatives are a key part of indefinite integrals.

Antidifferentiation
Finding the antiderivatives of a function require a little backwards thinking. Since the derivative of the wanted antiderivative is the given function, checking for correctness is easy. You just take the derivative, and see if it is the given function. Also, antiderivatives of functions happen to be not just one function, but a whole family of functions. This family can be written as a polynomial plus c, where c stands for any constant.

Custom Search