Volume in Geometry Examples
Related Topics:
More Lessons for High School Geometry
Math Worksheets
A series of free, online High School Geometry video, lessons and solutions.
Videos, worksheets, and activities to help Geometry students.
In this lesson, we will learn
- how to calculate the volume of a pyramid
- how to solve equations with squares and cubes
- how to calculate the volume of a sphere
- how to calculate the surface area of a sphere
Volume of a Pyramid
The volume of a pyramid is the amount of three-dimensional space it occupies. A pyramid is a solid formed by connecting a polygonal base and a single point, called the apex. The faces connecting the base to the apex are triangles.
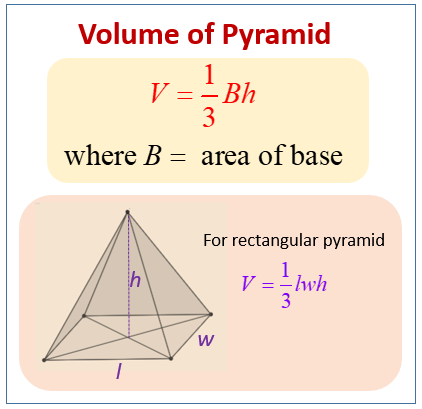
Formula for the Volume of a Pyramid
The following diagram gives the formula for volume of pyramid. Scroll down the page for more examples and solutions on how to use the volume of pyramid formula.
Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Geometry Worksheets
The general formula for the volume (V) of any pyramid is:
\(V = \frac{1}{3}\) × Area of the Base × height
\(V = \frac{1}{3}Ah\)
V = Volume of the pyramid
A = Area of the polygonal base of the pyramid. This will vary depending on the shape of the base (e.g., square, triangle, rectangle, pentagon).
h = height of the pyramid (the perpendicular distance from the apex to the plane of the base).
Explanation of the Formula Components
A: You must first calculate the area of the specific polygonal base.
h: This is the perpendicular height from the very top point (apex) of the pyramid straight down to the center of its base. It is not the slant height (the height of a triangular face).
\(\frac{1}{3}\): The volume of a pyramid is exactly one-third the volume of a prism that has the same base area and the same height.
Volume of Pyramid
The formula for the volume of prisms can also be applied to the volume of pyramids, which occupy only one third of the space of a corresponding prism with the same base and height. To calculate the volume of a pyramid, we simply multiply the area of the one of the bases times one third of the height of the pyramid. This formula is very similar to volume of cylinder and volume of cone formulas.
How to find the volume of a square pyramid and a triangular pyramid?
Also compare how they are the same and how they are different.
Find the volume of the pyramid
The formula for the volume of a pyramid is 1/3 x base x height.
Watch this video to discover how to use this formula to find the volume of a pyramid.
Solving Equations with Squares and Cubes
Many of the formulas for calculating volumes (prism volume, volume of cylinders, volume of cones formulas and volume of pyramids) require solving equations with square roots or cube roots. To solve these equations, we use many of the same principles that we learned when solving equations with square roots in Algebra such as isolating the unknown variable and simplifying
How to solve equations using square roots or cube roots.
Volume of Sphere
To find the volume of a sphere, we can calculate the volume by using a simple volume formula where we multiply 4/3 by pi by the radius cubed. The volume of sphere formula is unique because it only requires the radius to calculate the volume of any sphere. When finding the volume of spheres, it is important to note if we are given the radius or the diameter of the shape. This formula is very similar to other prism volume formulas.
Volume of a Sphere
How to calculate the volume of a sphere?
Surface Area of a Sphere
In general, surface area is the sum of all the shapes that cover the surface of an object. To calculate the surface area of a sphere we multiply 4 by pi by the radius of the sphere squared. Given this formula, we can find the surface area of a sphere when given the radius. Similarly, we can find the radius of a sphere is we are given the surface area. This formula is very similar to other prism volume formulas.
How to Find the Surface Area of a Sphere?
How to find the surface area of a sphere using the formula SA = 4(pi)(r)2?
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.