Volume with Fractional Edge Lengths and Unit Cubes
Lesson Plans and Worksheets for Grade 6
Lesson Plans and Worksheets for all Grades
More Lessons for Grade 6
Common Core For Grade 6
Videos, examples, and solutions to help Grade 6 students extend their understanding of the volume of a right rectangular prism with integer side lengths to right rectangular prisms with fractional side lengths. They apply the formula, V = l x w x h, to find the volume of a right rectangular prism and use the correct volume units when writing the answer.
New York State Common Core Math Grade 6, Module 5, Lesson 11
Grade 6, Module 5, Lesson 11 Worksheets (pdf)
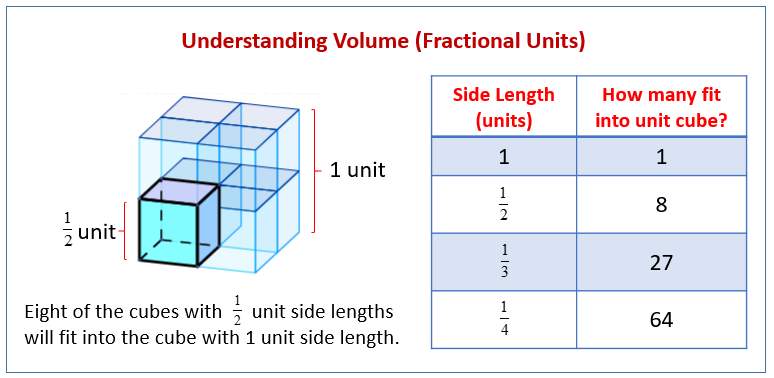
The following figure helps you to understand volume of cubes with fractional side lengths. Scroll down the page for examples and solutions.
Lesson 11 Opening Exercise
Which prism will hold more 1 in. × 1 in. × 1 in. cubes? How many more cubes will the prism hold?Example 1, Example 2
Exercises
2. Calculate the volume of the following rectangular prisms.
3. A toy company is packaging its toys to be shipped. Some of the very small toys are placed inside a cube shaped box with side lengths of 1/2 in. These smaller boxes are then packed into a shipping box with dimensions of 12 in. x 4 1/2 in. 3 1/2 in.
a. How many small toys can be packed into the larger box for shipping?
b. Use the number of toys that can be shipped in the box to help determine the volume of the box.
4. A rectangular prism with a volume of cubic units is filled with cubes. First it is filled with cubes with side lengths of 1/2 unit. Then it is filled with cubes with side lengths of 1/3 unit.
a. How many more of the cubes with 1/3 unit side lengths than cubes with 1/2 unit side lengths will be needed to fill the prism?
b. Why does it take more cubes with 1/3 unit side lengths to fill the prism?
5. Calculate the volume of the rectangular prism. Show two different methods for determining the volume.
Example 1
A box with the dimensions 10 in. by 4 in. by 6 in. will be used to ship miniature dice whose side lengths have been cut in half. The dice are are 1/2 in. x 1/2 in. x 1/2 in. cubes.
How many dice of this size can fit in the box?
A 1/4 in. cube is used to fill the prism. How many 1/4 in. cubes will it take to fill the prism? What is the volume of the prism? How is the number of cubes related to the volume?
Exercise 1
1. Use the prism to answer the following questions.
a. Calculate the volume.
b. If you have to fill the prism with cubes whose side lengths are less than 1 cm, what size would be best?
c. How many of the cubes would fit in the prism?
d. Use the relationship between the number of cubes and the volume to prove that your volume calculation is correct.
How to calculate how many half cubic or one third cubic units in a figure.
1. Answer the following questions using this rectangular prism:
a. What is the volume of the prism?
b. Linda fills the rectangular prism with cubes that have side lengths of 1/3 in. How many cubes does she need to fill the rectangular prism?
c. How is the number of cubes related to the volume?
d. Why is the number of cubes needed different from the volume?
e. Should Linda try to fill this rectangular prism with cubes that are 1/2 in. long on each side? Why or why not?
2. Calculate the volume of the following prisms.
3. A rectangular prism with a volume of 12 cubic units is filled with cubes twice: once with cubes with 1/2-unit side lengths and once with cubes with 1/3-unit side lengths.
a. many more of the cubes with 1/3-unit side lengths than cubes with 1/2-unit side lengths are needed to fill the prism?
b. Finally, the prism is filled with cubes whose side lengths are 1/4 unit. How many 1/4-unit cubes would it take to fill the prism?
4. A toy company is packaging its toys to be shipped. Each toy is placed inside a cube-shaped box with side lengths of 3 1/2 in. These smaller boxes are then packed into a larger box with dimensions of 14 in × 7 in. × 3 1/2 in.
a. What is the greatest number of toy boxes that can be packed into the larger box for shipping?
b. Use the number of toy boxes that can be shipped in the large box to determine the volume of the shipping box.
5. A rectangular prism has a volume of 34.224 cubic meters. The height of the box is 3.1 meters, and the length is 2.4 meters.
a. Write an equation that relates the volume to the length, width, and height. Let w represent the width, in meters.
b. Solve the equation.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.