Set Operations - Union, Intersection, Complement

In mathematics, sets are well-defined collections of distinct objects, called elements. We will look at the following set operations: Union, Intersection and Complement.

Basic Set Notation
A set is an unordered collection of unique elements, denoted by capital letters (e.g. A,B).
Elements are listed within curly braces: A={1,2,3}.
Universal Set (U): Contains all possible elements in a context.
Empty Set (∅): A set with no elements.

The following figures give the set operations and Venn Diagrams for complement, subset, intersection, and union. Scroll down the page for more examples and solutions.

 

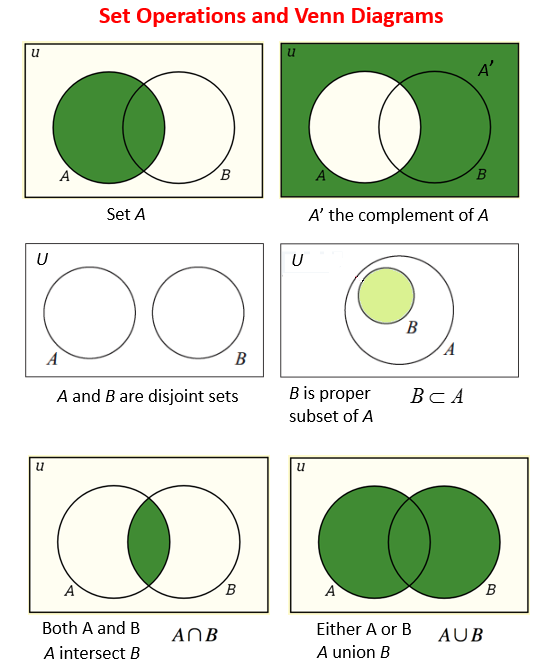
Key Set Operations
1. Union (∪)
Definition: The union of two sets A and B is the set containing all elements that are in A, or in B, or in both. Duplicates are not listed.
Symbol: A ∪ B
Venn Diagram: The entire shaded area of both circles.

2. Intersection (∩)
Definition: The intersection of two sets A and B is the set containing only the elements that are common to both A and B.
Symbol: A ∩ B
Venn Diagram: The overlapping shaded area of the two circles.

3. Complement (A′ or A^c)
Definition: The complement of a set A (relative to a universal set U) is the set of all elements in U that are not in A.
Venn Diagram: The shaded area outside of circle A, but within U.

4. Subset
Definition: Set A is a subset of a set B if every element of A is also an element of B.
There are two primary symbols used to denote subsets:
⊆ (Is a subset of / Is included in)
This symbol means that set A is a subset of set B, and it includes the possibility that A and B are exactly the same set.
Read as: “A is a subset of B” or “A is contained in B."

⊂ (Is a proper subset of / Is strictly included in)
This symbol means that set A is a subset of set B, AND A is not equal to B. In other words, B must contain at least one element that is not in A.
Read as: “A is a proper subset of B.”

Videos

Intersection of Sets, Union of Sets and Venn Diagrams

This video gives an introduction into the intersection of sets and union of sets as it relates to Venn diagrams. It explains how to find the intersection of two sets as well as the union of two sets. This video contains plenty of examples and practice problems on intersection and union of sets.

• Show Video Lesson

Intersection of Sets
Learn about intersection of sets.

Example:
Set A = {1, 4, 6, 8}
Set B = {0, 2, 4, 8, 9}
U = {the digits}
Draw a Venn Diagram for A ∩ B

• Show Video Lesson

Complement of a Set
Learn what a complement of a set is.

Example:
Set A = {0, 1, 4, 5, 6, 7, 8}
U = {the digits}
Draw a Venn Diagram for A'

• Show Video Lesson

Boolean Set Operations
Intersection, union and complement set operations defined

Example:
Universe = {1,2,3,4,5,6,7,8,9,10}
A = {2,4,6,8,10}
B = {6,7,8,9,10}

• Show Video Lesson

Sets - Intersection, Union and Complement
A ∩ B pronounced as A intersection B are members that are common to both set A and set B.
A ∪ B pronounced as A union B are members that are in set A or set B or both.
A’ pronounced as A complement are members that are not in set A.

Example:
If U = {1,2,3,4,5,6,7,8,9,10}
A = {1,2,3,4,5,6}
B = {1,2,3,5,7}
C = {2,4} and D = {8,9}

Find
A ∩ B
A ∪ B
A’
A ∩ C
A ∪ C
B ∩ D
B ∪ D
B’
A ∩ B ∩ C
(A ∪ B)'

• Show Video Lesson

Set Operations and Venn Diagrams - Part 1 of 2
A Venn diagram is a visual diagram that shows the relationship of sets with one another.
The set of all elements being considered is called the universal set (U) and is represented by a rectangle.
The complement of A, A’, is the set of elements in U but not in A. A’ = {x|x ∈ U and x = ∉ A}
Set A and B are disjoint because they do not share any common elements.
B is a proper subset of A. This means B is a subset of A, but B ≠ A.
The intersection A and B is the set of elements in both set A and set B.
The union of A and B is the set of elements in set A or set B.
Intersection and Unions with the Empty Set
A ∩ ∅ = ∅
A ∪ ∅ = A

• Show Video Lesson

Set Operations and Venn Diagrams - Part 2 of 2

Examples:

1. Create a Venn diagram to show the relationship among the sets.
   U is the set of whole numbers from 1 to 15.
   A is the set of multiples of 3.
   B is the set of primes.
   C is the set of odd numbers

2. Given the following Venn diagram, determine each of the following sets.
   a. A ∩ B.
   b. A ∪ B
   c. (A ∪ B)’
   d. A’ ∩ B
   e. A ∪ B'

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.