Review of Transformations
Related Topics:
More Lessons for High School Regents Exam
Math Worksheets
High School Math based on the topics required for the Regents Exam conducted by NYSED.
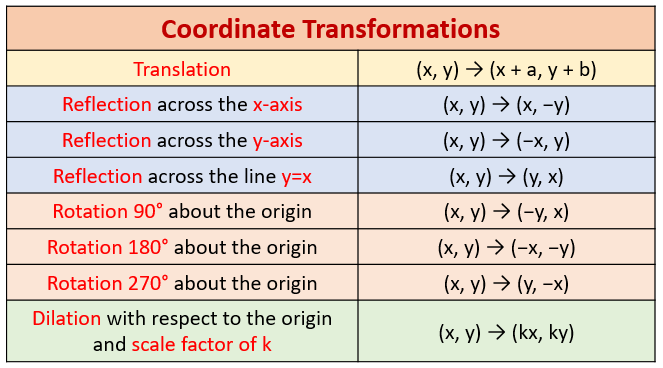
The following diagrams show transformations on the coordinate plane, reflection, rotation, translation, dilation. Scroll down the page for more examples and solutions on the coordinate transformations.
A reflection is a flip.
It is an opposite isometry. This means that the image does not change size but the lettering is reversed.
Reflection in the x-axis: Rx-axis (x, y) = (x, -y)
Reflection in the y-axis: Ry-axis(x, y) = (-x, y)
Reflection in the line y = x: Ry = x(x, y) = (y, x)
Reflection in the line y = -x, Ry = -x(x, y) = (-y, -x)
A rotation turns a figure through an angle about a fixed point called the center.
A positive angle of rotation turns the figure counterclockwise, and a negative angle of rotation turns the figure in a clockwise direction. It is a direct isometry - the order of the lettering in the figure and the image are the same.
Rotation of 90° about the origin: R90°(x, y) = (-y, x)
Rotation of 180° (or point rotation about the origin) : R180°(x, y) = (-x, -y)
Rotation of 270° about the origin : R270°(x, y) = (y, -x)
A translation “slides” an object a fixed distance in a given direction.
The original object and its translation have the same shape and size, and they face in the same direction. It is a direct isometry - the order of the lettering in the figure and the image are the same.
Translation of h, k : Th,k(x, y) = (x+h, y+k)
A dilation is a transformation that produces an image that is the same shape as the original, but is a different size. It is not an isometry and it forms similar figures.
Dilation of scale factor k with the center at the origin: Dk(x, y) = (kx, ky)
Transformations - Reflection
Review the rules for performing a reflection across the x-axis.
When reflecting an object over the x-axis, keep all x-values and change the y-value. This tutorial reviews how to perform a reflection over the x-axis on the coordinate plane.
Transformations - Rotate 90 degrees
This video reviews how to perform 90 degree rotations (clockwise and counterclockwise) around the origin.
Rotate 180 Degrees Around The Origin
This tutorial shows why all signs of an ordered pair of an object become opposite when rotating that object 180 degrees around the origin.
Transformations - Translating a Polygon On The Coordinate Plane
This tutorial reviews how to translate a given polygon on the coordinate plane.
Dilation Of Objects On The Coordinate Plane
This tutorial reviews how to dilate an object on the coordinate plane when the center of dilation is the origin and also when the center of dilation is not the origin.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.