Surface Area of Solids using Nets
Related Pages
Surface Area Formula
Surface Area of Prisms
Surface Area of a Sphere
More Geometry Lessons
Geometry Worksheets
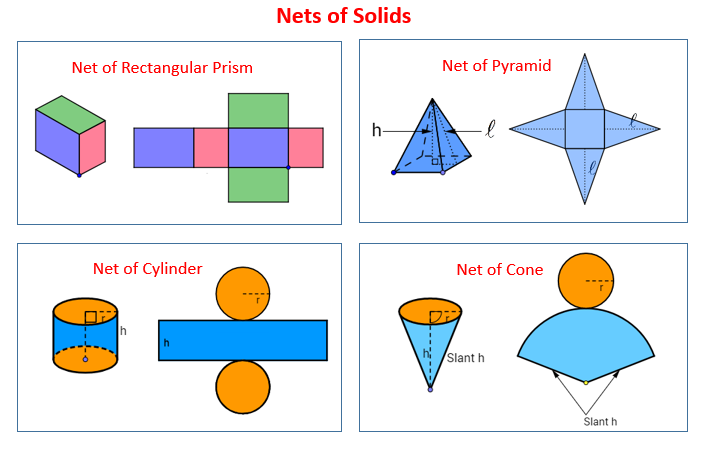
In these lessons, we will look at using nets to calculate the surface area of a cube, rectangular prism or cuboid, triangular prism, cylinder, pyramid and cone.
The following diagrams show the nets of rectangular prism, pyramid, cylinder and cone. Scroll down the page for more examples and solutions.
Printable & Online Surface Area Worksheets
Nets of a Solid
A net is a pattern made when the surface of a three-dimensional figure or solid is laid out flat showing each face of the figure. It is then possible to use the net to calculate the surface area of the solid.
Surface Area of a Cube using Nets
A cube is a three-dimensional figure with six matching square faces.
The following nets can be folded along the dotted lines to form a cube.
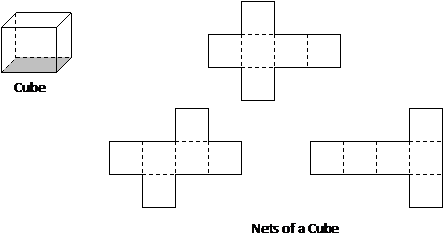
For example, if the length of one side of the cube 3 units then the area of one its face is 3 × 3 = 9 units2. From the net, we can see that there are six equal faces and so we get the total surface area is 6 × 9 = 54 units2.
Surface Area of a Rectangular Prism using Nets
A rectangular prism or cuboid is formed by folding a net as shown:
We can see from the net that there are two rectangles with dimensions 3 cm by 6 cm, two rectangles with dimensions 2 cm by 6 cm and two rectangles with dimensions 2 cm by 3 cm. The total surface area is then
2 × 3 × 6 + 2 × 2 × 6 + 2 × 2 × 3 = 72 cm2
How to find the surface area of a rectangular prism when its net is given?
How to find the surface area of a rectangular prism using nets?
Surface Area of a Triangular Prism using Nets
How to find the surface area of a triangular prism using nets?
How to calculate the surface area of a triangular prism by first drawing a net for the prism?
Surface Area of a Cylinder using Nets
How to find the surface area of a cylinder by drawing the net?
Surface Area of a Pyramid using Nets
How to find the surface area of a pyramid and a cylinder by drawing the nets?
Surface Area of a Hexagonal Prism using Nets
How to find the surface area of a hexagonal prism by drawing a net?
Surface Area of a Cone
How to find the surface area and volume of a right circular cone?
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.