Surface Area of Solids
Related Topics:
More Lessons for High School Geometry
More Lessons for Geometry
Math Worksheets
A series of free, online High School Geometry Videos, Lessons and solutions.
Examples, solutions, videos, worksheets, and activities to help Geometry students.
Surface Area = 2 × Base + height × perimeter
S.A. = 2B + hp
Surface Area of Prisms
Surface area is a two-dimensional property of a three-dimensional figure. Prisms have two congruent, parallel bases separated by lateral faces. Lateral faces are congruent rectangles with a height equal to the prism, unless oblique, and bases equal to the side lengths of the congruent bases. Therefore, to find the surface area of prisms, find the area of the bases and the lateral faces and sum them.
How to calculate the surface area of any right prism?
Deriving and using the formula for the surface area of a right prism. Step by step procedure to finding surface area of a rectangular prism.
Surface Area of Cylinders
Surface area is a two-dimensional property of a three-dimensional figure. Cylinders are similar to prisms in that they have congruent, parallel bases, except cylinders have circles as their bases. To conceptualize surface area of cylinders, we can imagine that the lateral area of a cylinder can be "unrolled" into a rectangle with one side equals to the circumference of the circle and the other side equal to the height of the cylinder (unless it is oblique).
How to prove the surface area of a cylinder formula?
How to find the surface area of a cylinder?
Surface Area of a Pyramid
Surface area is a two-dimensional property of a three-dimensional figure. Pyramids have polygonal bases and triangular faces, which are congruent if the base is regular. To find the total surface area of a pyramid, first find the area of the base and then find the area of each triangular faces. The height of each triangle is called the slant height. Related topics include regular polygonal area and triangle area.
How to calculate the surface area of any pyramid, emphasizing regular polygons as bases?
How to Find the Surface Area of a Regular Pyramid?
More Lessons for High School Geometry
More Lessons for Geometry
Math Worksheets
A series of free, online High School Geometry Videos, Lessons and solutions.
Examples, solutions, videos, worksheets, and activities to help Geometry students.
In this lesson, we will learn
- how to calculate the surface area of prisms
- how to calculate the surface area of cylinders
- how to calculate the surface area of pyramids
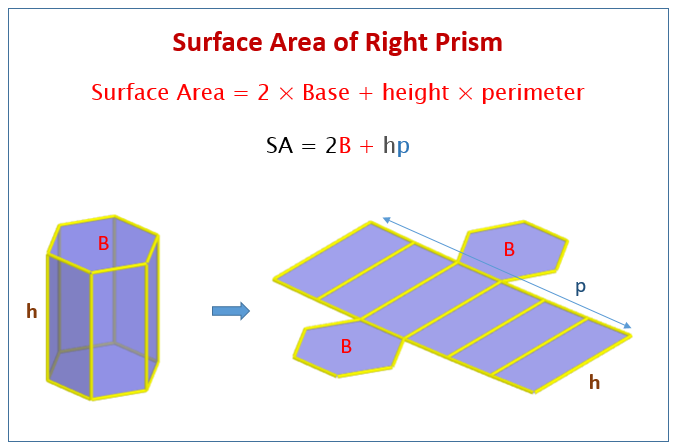
Surface Area = 2 × Base + height × perimeter
S.A. = 2B + hp
Surface Area of Prisms
Surface area is a two-dimensional property of a three-dimensional figure. Prisms have two congruent, parallel bases separated by lateral faces. Lateral faces are congruent rectangles with a height equal to the prism, unless oblique, and bases equal to the side lengths of the congruent bases. Therefore, to find the surface area of prisms, find the area of the bases and the lateral faces and sum them.
How to calculate the surface area of any right prism?
Deriving and using the formula for the surface area of a right prism. Step by step procedure to finding surface area of a rectangular prism.
Surface area is a two-dimensional property of a three-dimensional figure. Cylinders are similar to prisms in that they have congruent, parallel bases, except cylinders have circles as their bases. To conceptualize surface area of cylinders, we can imagine that the lateral area of a cylinder can be "unrolled" into a rectangle with one side equals to the circumference of the circle and the other side equal to the height of the cylinder (unless it is oblique).
How to prove the surface area of a cylinder formula?
How to find the surface area of a cylinder?
Surface area is a two-dimensional property of a three-dimensional figure. Pyramids have polygonal bases and triangular faces, which are congruent if the base is regular. To find the total surface area of a pyramid, first find the area of the base and then find the area of each triangular faces. The height of each triangle is called the slant height. Related topics include regular polygonal area and triangle area.
How to calculate the surface area of any pyramid, emphasizing regular polygons as bases?
How to Find the Surface Area of a Regular Pyramid?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.