Surface Area of Similar Figures

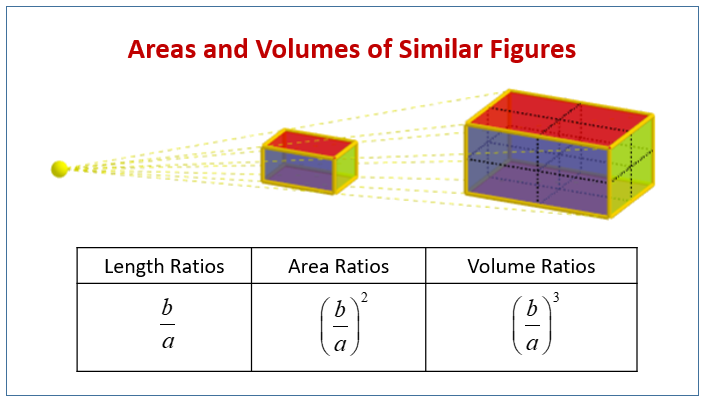
Area and Volume of Similar Figures: Scaling Rules

When dealing with similar figures (or solids), there’s a relationship between their linear dimensions (like side lengths, radii, heights), their areas, and their volumes. This relationship is governed by the scale factor.

The following diagram shows how the length ratios, area ratios and volume ratios of similar figures are related. Scroll down the page for more examples and solutions.

What are Similar Figures/Solids?
Two figures or solids are similar if they have the same shape but possibly different sizes. One is an enlargement or reduction of the other.

1. Corresponding angles are equal.
2. Corresponding linear dimensions (sides, heights, radii, diagonals) are in proportion. This common ratio is called the linear scale factor.

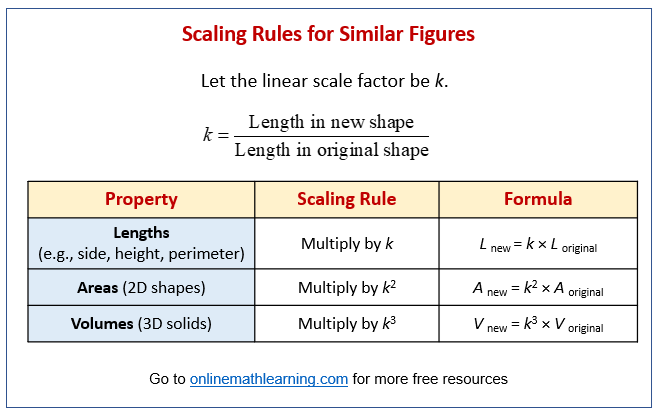
Formula for the Linear Scale Factor (k)

\(k = \frac{\text{Length in new shape}}{\text{Length in original shape}}\).

Scaling Rules for Similar Figures

The following diagram shows scaling rules and formulas for similar figures. Scroll down the page for more examples and solutions.

Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Geometry Worksheets

This relationship is useful for solving problems involving similar shapes without needing to calculate all individual dimensions.

Example (Area):
A small triangle has an area of 10 cm². A larger triangle is similar to the first, and its sides are twice as long as the small triangle’s sides. What is the area of the larger triangle?
Solution:
Linear scale factor k=2.
Area of small triangle A₁ =10cm².
Area of large triangle A₂ = k² × A₁ = 2²×10=4×10=40cm².

Example (Volume):
A small sphere has a radius of 3 cm and a volume of 36πcm³. A larger sphere is similar and has a radius of 6 cm. What is the volume of the larger sphere?
Solution:
Linear scale factor \(k = \frac{\text{Radius of large sphere}}{\text{Radius of small sphere}}=\frac{6 cm}{3 cm} = 2\)
Volume of small sphere V₁ = 36πcm³
Volume of large sphere V₂ = k³ × V₁ = 2³×36π=8×36π=288πcm³.

Surface Areas and Volumes of Similar Solids
Learn about the effect of changing dimensions on Surface Areas and volumes

• Show Video Lesson

Ratios of Perimeters and Ratios of Area
This video explains how to find the ratio of areas and ratios of perimeters for similar polygons

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.