Supplementary Angles
Related Topics:
More Lessons for Grade 6 Math
Math Worksheets
Examples, solutions, videos, worksheets, stories, and songs to help Grade 6 students learn about supplementary angles.
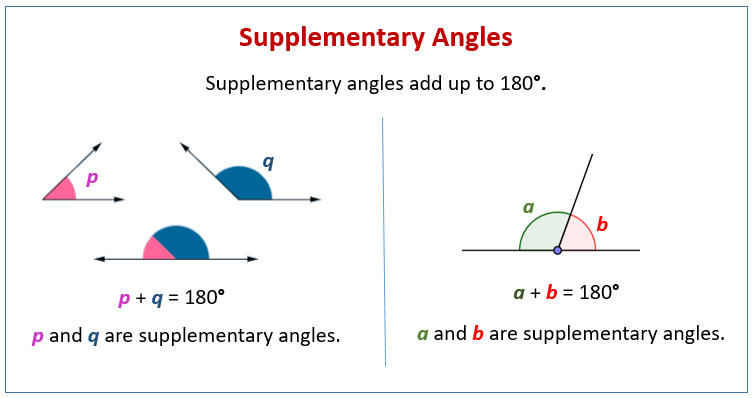
What are Supplementary Angles?
Two angles are supplementary if they add up to 180°. Supplementary angles, when placed adjacent to each other, form a straight line, a 180° angle. Do note however that supplementary angles do not have to be adjacent to each other, they need only to have an angle measure sum of 180 degrees.
The following diagrams show examples of supplementary angles. Scroll down the page for more examples and solutions for supplementary angles.
Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Geometry Worksheets
Key Characteristics of Supplementary Angles:
1. Sum is 180°:
If you have two angles, say Angle A and Angle B, they are supplementary if:
Measure of Angle A + Measure of Angle B = 180°
2. Linear Pair (when adjacent):
If two supplementary angles are placed next to each other (i.e., they share a common vertex and a common side), they form a linear pair. A linear pair always forms a straight line.
Supplementary Angles add up to 180 Degrees
Supplementary Angles
It is common to mix up supplementary and complementary angles. Here is a trick to help you remember which is which:
The “C” and “S” Trick
Complementary: Think C for Corner. A corner (like of a square or a table) is a right angle, which is 90 degrees.
Supplementary: Think S for Straight. A straight line forms a straight angle, which is 180 degrees.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.