

Factoring the Sum and Difference of Two Cubes
Related Topics:
More Grade 9 Math Lessons
More Algebra I Lessons
More Algebra II Lessons
Algebra Worksheets
Algebra Games
Examples, videos, worksheets, solutions, and activities to help Grade 9, Algebra students learn how to factor the sum of two cubes and the difference of two cubes.
The following diagrams show how to factor the sum or difference of two cubes. Scroll down the page for more examples and solutions of using the formula to factor the sum of cubes or the difference of cubes.
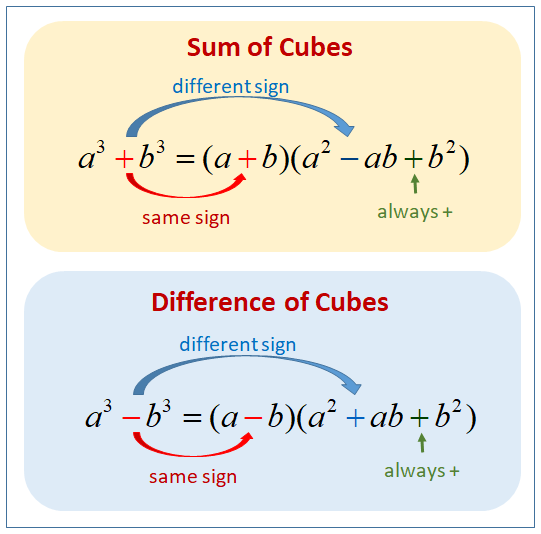
Formula to Factor the Sum of two Cubes
a3 + b3 = (a + b)(a2 − ab + b2)
Factoring by Grouping.
Algebra - Sum and Difference of Cubes Part 1 Intuitive Math Help
Algebra - Sum and Difference of Cubes Part 2 Intuitive Math Help
Algebra - Sum and Difference of Cubes Part 3/3- Intuitive Math Help



More Grade 9 Math Lessons
More Algebra I Lessons
More Algebra II Lessons
Algebra Worksheets
Algebra Games
Examples, videos, worksheets, solutions, and activities to help Grade 9, Algebra students learn how to factor the sum of two cubes and the difference of two cubes.
The following diagrams show how to factor the sum or difference of two cubes. Scroll down the page for more examples and solutions of using the formula to factor the sum of cubes or the difference of cubes.

Formula to Factor the Sum of two Cubes
a3 + b3 = (a + b)(a2 − ab + b2)
Formula to Factor the Difference of two Cubes
a3 − b3 = (a − b)(a2 + ab + b2)
Factoring by Grouping.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.