Special Right Triangles
Related Topics:
More Lessons for Grade 8
Math Worksheets
Videos, worksheets, stories, and solutions to help Grade 8 students learn about the special right triangles: 45-45-90, 30-60-90.
Special Triangles
In geometry, “special triangles” typically refer to triangles that have unique properties, particularly predictable relationships between their angles and side lengths. These relationships make calculations faster and often lead to exact solutions. While all triangles have special properties (like the sum of angles being 180 degrees), the term “special triangles” most commonly refers to special right triangles.
There are two main types of special right triangles:
- 45-45-90 Triangle
- 30-60-90 Triangle
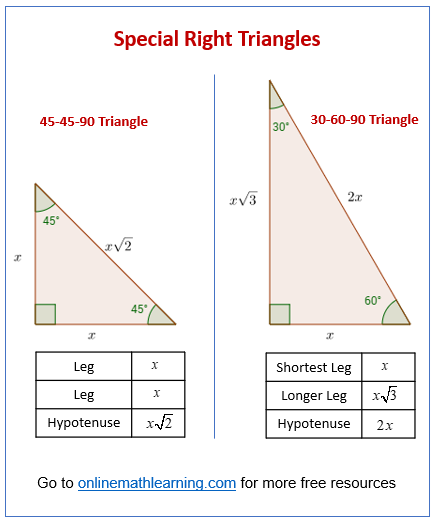
The following figures show the special right triangles and the ratio of their sides. Scroll down the page if you need more explanations and examples of special right triangles.
Geometry Worksheets
Practice your skills with the following geometry worksheets:
Printable & Online Geometry Worksheets
1. The 45-45-90 Triangle (Isosceles Right Triangle)
This triangle is characterized by its angles: 45 degrees, 45 degrees, and 90 degrees. Because two of its angles are equal (45°), it is an isosceles triangle, meaning the two legs (the sides opposite the 45° angles) are congruent.
Side Ratios:
Leg : Leg : Hypotenuse
\(x : x : \sqrt{2} \)
How to Use It:
If you know the length of one side of a 45-45-90 triangle, you can find the others:
a) Given a Leg: If a leg is 5 units, then the other leg is also 5 units, and the hypotenuse is \(5\sqrt{2}\) units.
b) Given the Hypotenuse: If the hypotenuse is 10 units, then each leg is \(\frac{10}{\sqrt{2}}\) units.
2. The 30-60-90 Triangle
This triangle has angle measures of 30 degrees, 60 degrees, and 90 degrees. The side lengths are in a specific ratio relative to the angle they are opposite.
Side Ratios:
Side opposite 30° (Short Leg) : Side opposite 60° (Long Leg) : Side opposite 90° (Hypotenuse)
\(x : x\sqrt{3} : 2x \)
How to Use It:
If you know the length of just one side of a 30-60-90 triangle, you can find the lengths of the other two sides:
a) Given the Shortest Leg (x): If the side opposite 30° is 4, then the hypotenuse is 2×4=8, and the side opposite 60° is \(4\sqrt{3}\).
b) Given the Hypotenuse (2x): If the hypotenuse is 12, then the side opposite 30° is 12/2=6, and the side opposite 60° is \(6\sqrt{3}\).
c) Given the Longest Leg (\(x\sqrt{3}\)): If the side opposite 60° is \(9\sqrt{3}\), then the side opposite 30° is 9. The hypotenuse is 2×9=18.
Special Right Triangles: 30-60-90 and 45-45-90 Triangles
In this video, students learn that in a 45-45-90 triangle, the legs are congruent, and the length of the hypotenuse is equal to root 2 times the length of a leg. Students also learn that in a 30-60-90 triangle, the length of the long leg is equal to root 3 times the length of the short leg, and the length of the hypotenuse is equal to 2 times the length of the short leg.
Special Right Triangles in Geometry: 45-45-90 and 30-60-90 degree triangles
This video discusses two special right triangles, how to derive the formulas to find the lengths of the sides of the triangles by knowing the length of one side, and then do a few examples using them!
Find Sides of 45-45-90 and 30-60-90 Right Triangles
If you are given one side of a 45-45-90 triangle or one side of a 30-60-90 triangle you have enough information to solve for each of the two missing sides.
This video shows how to do it going from smaller sides to larger sides and larger sides to smaller sides. It also shows how the found sides can be used to find the perimeter and area of the right triangle.
Special Right Triangle Explanation
Explaining How to find the missing sides of right triangles using the relationships of sides for 30-60-90 right triangles, 45-45-90 right triangles, and 3-4-5 right triangles
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.