Graph Equations using Slope and Intercept
Related Topics:
Lesson Plans and Worksheets for Grade 8
Lesson Plans and Worksheets for all Grades
More Lessons for Grade 8
Common Core For Grade 8
Videos, examples, and solutions to help Grade 8 students learn how to graph equations in the form of y = mx + b using information about slope and y-intercept.
• Students know that if they have two straight lines with the same slope and a common point that the lines are the same.
• The equation y = mx + b is in slope-intercept form. The number m represents the slope of the graph and the point (0,b) is the location where the graph of the line intersects the y-axis.
• To graph a line from the slope-intercept form of a linear equation, begin with the known point, (0, b), then use the slope to find a second point. Connect the points to graph the equation.
• There is only one line passing through a given point with a given slope.
Lesson 18 Opening Exercise
Examine each of the graphs and their equations below. Identify the coordinates of the point where the line intersects the y-axis. Describe the relationship between the point and the equation y = mx + b.
Standard Form of a linear equation: ax + by + c = 0
Slope-Intercept Form of a linear equation: y = mx + b
Example 1
Graph the equation y = 2/3 x + 1. Name the slope and y-intercept.
Example 2
Graph the equation y = -3/4 x - 2. Name the slope and y-intercept.
Example 3
Graph the equation y = 4x - 7. Name the slope and y-intercept.
Exercises 1–4
1. Graph the equation y = 5/2 x - 4.
a. Name the slope and y-intercept.
b. Graph the known point, then use the slope to find a second point before drawing the line.
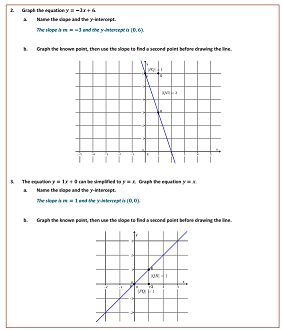
2. Graph the equation y = -3x + 6.
a. Name the slope and y-intercept.
b. Graph the known point, then use the slope to find a second point before drawing the line.
3. The equation y = 1x simplifies to y = x. Graph the equation y = x.
a. Name the slope and y-intercept.
b. Graph the known point, then use the slope to find a second point before drawing the line.
4. Graph the point (0, 2).
a. Find another point on the graph using the slope, m = 2/7.
b. Connect the points to make the line.
c. Draw a different line that goes through the point (0, 2) with slope 2/7. What do you notice?
Exercises 5–6
5. A bank put $10 into a savings account when you opened the account. Eight weeks later you have a total of $24. Assume you saved the same amount every week.
a. If y is the total amount of money in the savings account and x represents the number of weeks, write an equation in the form y = mx + b that describes the situation.
b. Identify the slope and the y-intercept. What do these numbers represent?
c. Graph the equation on a coordinate plane.
d. Could any other line represent this situation? For example, could a line through point (0, 100 with slope 7/5 represent the amount of money you save each week? Explain.
6. A group of friends are on a road trip. So far they have driven 120 miles. They continue their trip and drive at a constant rate of 50 miles per hour.
a. Let y represent the total distance traveled in x hours. Write an equation to represent the total number of miles driven in x hours.
b. Identify the slope and the y-intercept. What do these numbers represent?
c. Graph the equation on a coordinate plane.
d. Could any other line represent this situation? For example, could a line through point (0, 120) with slope 75 represent the total distance the friends drive? Explain.
Lesson Plans and Worksheets for Grade 8
Lesson Plans and Worksheets for all Grades
More Lessons for Grade 8
Common Core For Grade 8
Videos, examples, and solutions to help Grade 8 students learn how to graph equations in the form of y = mx + b using information about slope and y-intercept.
New York State Common Core Math Grade 8, Module 4, Lesson 18
Download Worksheets for Grade 8, Module 4, Lesson 18
Lesson 18 Student Outcomes
• Students graph equations in the form of y = mx + b using information about slope and y-intercept.• Students know that if they have two straight lines with the same slope and a common point that the lines are the same.
Lesson 18 Summary
• The equation y = mx + b is in slope-intercept form. The number m represents the slope of the graph and the point (0,b) is the location where the graph of the line intersects the y-axis.
• To graph a line from the slope-intercept form of a linear equation, begin with the known point, (0, b), then use the slope to find a second point. Connect the points to graph the equation.
• There is only one line passing through a given point with a given slope.
Lesson 18 Opening Exercise
Examine each of the graphs and their equations below. Identify the coordinates of the point where the line intersects the y-axis. Describe the relationship between the point and the equation y = mx + b.
Standard Form of a linear equation: ax + by + c = 0
Slope-Intercept Form of a linear equation: y = mx + b
Example 1
Graph the equation y = 2/3 x + 1. Name the slope and y-intercept.
Example 2
Graph the equation y = -3/4 x - 2. Name the slope and y-intercept.
Example 3
Graph the equation y = 4x - 7. Name the slope and y-intercept.
1. Graph the equation y = 5/2 x - 4.
a. Name the slope and y-intercept.
b. Graph the known point, then use the slope to find a second point before drawing the line.
2. Graph the equation y = -3x + 6.
a. Name the slope and y-intercept.
b. Graph the known point, then use the slope to find a second point before drawing the line.
3. The equation y = 1x simplifies to y = x. Graph the equation y = x.
a. Name the slope and y-intercept.
b. Graph the known point, then use the slope to find a second point before drawing the line.
4. Graph the point (0, 2).
a. Find another point on the graph using the slope, m = 2/7.
b. Connect the points to make the line.
c. Draw a different line that goes through the point (0, 2) with slope 2/7. What do you notice?
Exercises 5–6
5. A bank put $10 into a savings account when you opened the account. Eight weeks later you have a total of $24. Assume you saved the same amount every week.
a. If y is the total amount of money in the savings account and x represents the number of weeks, write an equation in the form y = mx + b that describes the situation.
b. Identify the slope and the y-intercept. What do these numbers represent?
c. Graph the equation on a coordinate plane.
d. Could any other line represent this situation? For example, could a line through point (0, 100 with slope 7/5 represent the amount of money you save each week? Explain.
6. A group of friends are on a road trip. So far they have driven 120 miles. They continue their trip and drive at a constant rate of 50 miles per hour.
a. Let y represent the total distance traveled in x hours. Write an equation to represent the total number of miles driven in x hours.
b. Identify the slope and the y-intercept. What do these numbers represent?
c. Graph the equation on a coordinate plane.
d. Could any other line represent this situation? For example, could a line through point (0, 120) with slope 75 represent the total distance the friends drive? Explain.
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.