Find the Slope given two points
Related Topics:
More Lessons for Grade 8
Math Worksheets
Examples, solutions, videos, worksheets, and lessons to help Grade 8 students learn how to find the slope of a line given two points.
The slope formula is a fundamental tool in algebra used to calculate the steepness and direction of a straight line. It quantifies how much a line rises or falls for every unit it moves horizontally.
The following diagram shows the slope formula when given two points on a line. Scroll down the page for more examples and solutions for the slope formula.
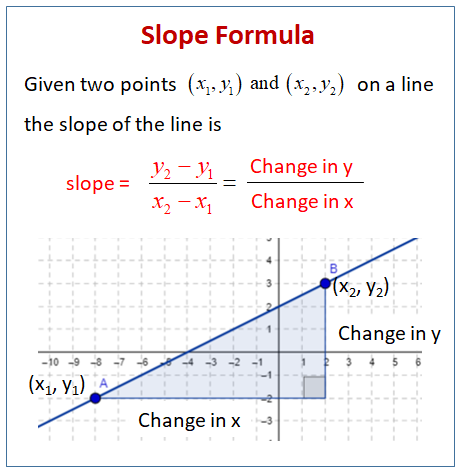
Coordinate Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Coordinate Geometry Worksheets
The Formula:
Given two distinct points on a line, \(x_1, y_1\) and \(x_2, y_2\), the slope \(m\) of the line passing through these points is calculated using the following formula:
\(m = \frac{y_2 - y_1}{x_2 - x_1}\)
where:
\(m\): Represents the slope of the line.
\(y_2 - y_1\): Represents the vertical change between the two points, often referred to as the “rise” \((\Delta y)\).
\(x_2 - x_1\): Represents the horizontal change between the two points, often referred to as the “run” \((\Delta x)\).
How to Use the Slope Formula:
- Determine the coordinates of any two distinct points that lie on the line. Label them as \(x_1, y_1\) and \(x_2, y_2\). It doesn’t matter which point you label as the first or second, as long as you are consistent with your subtraction in the numerator and the denominator.
- Plug the x and y values of the two points into the slope formula. Make sure to subtract the y-coordinates in the numerator and the corresponding x-coordinates in the denominator in the same order.
- Perform the subtraction in the numerator and the denominator, and then divide the result to find the value of the slope \((m)\).
Example 1: Finding the slope given two points
Find the slope of the line passing through the points (-2, 1) and (3, 5).
Let \((x_1, y_1) = (−2,1)\) and \((x_2, y_2) = (3,5)\).
\(m = \frac{5 - 1}{3 - (-2)} = \frac{4}{5}\)
The slope of the line is \(\frac{4}{5}\).
This positive slope indicates that the line goes upwards from left to right.
Example 2: Finding the slope with a negative change
Find the slope of the line passing through the points (4, -2) and (1, 4).
Let \((x_1, y_1) = (4,-2)\) and \((x_2, y_2) = (1,4)\).
\(m = \frac{4 - (-2)}{1 - 4} = \frac{6}{-3} = -2\)
The slope of the line is -2.
This negative slope indicates that the line goes downwards from left to right.
Example 3: Horizontal Line
Find the slope of the line passing through the points (-1, 3) and (2, 3).
Let \((x_1, y_1) = (-1,3)\) and \((x_2, y_2) = (2,3)\).
\(m = \frac{3 - 3}{2 - (-1)} = \frac{0}{3} = 0\)
The slope of a horizontal line is always 0 because there is no vertical change.
Example 4: Vertical Line
Find the slope of the line passing through the points (2, -4) and (2, 1).
Let \((x_1, y_1) = (2,-4)\) and \((x_2, y_2) = (2,1)\).
\(m = \frac{1 - (-4)}{2 - 2} = \frac{5}{0}\)
The slope of a vertical line is undefined because there is no horizontal change, and division by zero is not defined.
Finding the Slope Given 2 Points
How to Find the Slope Given 2 Points?
Calculating Slope using two points
Step-by-step procedure for calculating the slope of a line using two points on the line.
The Slope Formula
In this lesson, students are given the coordinates of two points, and are asked to find the slope of the line that passes through the points (without graphing). To solve the problems in this lesson, students use the slope formula, which states that m = (y2 - y1) / (x2 - x1). The slope formula can be read as “slope equals the second y coordinate minus the first y-coordinate over the second x-coordinate minus the first x-coordinate”.
Finding the Slope of a Line Through Two Points
The following shows two examples of finding the slope of a line through two points.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.