Similarity and Trig Ratios
Related Topics:
Common Core (Geometry)
Common Core for Mathematics
Examples, solutions, videos, and lessons to help High School students learn how to understand that by similarity, side ratios in right triangles are properties of the angles in the triangle, leading to definitions of trigonometric ratios for acute angles.
Common Core: HSG-SRT.C.6
The following diagram shows the connection between trigonometry and similar triangles. Scroll down the page for more examples and solutions for trig ratios and similar triangles.
Using similarity to define sine, cosine, and tangent
Connections between similar triangles and trigonometry.
Trig and similar triangles
Labeling Sides
Learn how to label the sides of a right triangle as 'hypotenuse', 'opposite', and 'adjacent' in relation to one of the triangle's acute angles. Writing Trig Ratios
Writing the basic trig ratios given three side lengths; or given two side lengths. Writing Ratios part 1
Learn how to write the three primary trig. ratios for a right triangle given the three side lengths. Writing Ratios part 2
Learn how to write the three primary trig. ratios for a right triangle given two of the three side lengths. Finding a Side Using Trig
Using the tangent function to find an unknown side in a right triangle - two examples... one where the missing side ends up on the top of the ratio in the trig equation, and another where it ends up on the bottom. Finding an Angle Using Trig
Using the inverse tangent function to find an angle in a right. Trigonometric Ratios on a Calculator
Introduction to the trig function buttons (SIN,COS,TAN), and inverse function buttons (INVERSE SIN,COS,TAN) on a calculator.
Common Core (Geometry)
Common Core for Mathematics
Examples, solutions, videos, and lessons to help High School students learn how to understand that by similarity, side ratios in right triangles are properties of the angles in the triangle, leading to definitions of trigonometric ratios for acute angles.
Common Core: HSG-SRT.C.6
The following diagram shows the connection between trigonometry and similar triangles. Scroll down the page for more examples and solutions for trig ratios and similar triangles.
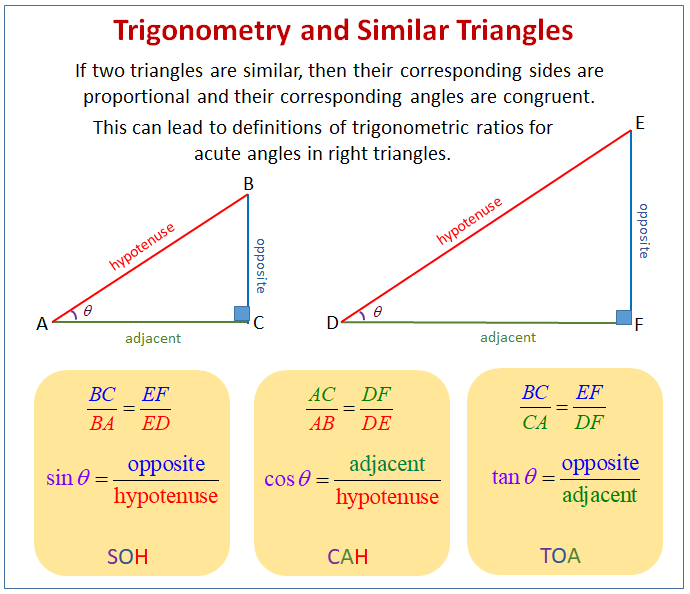
Using similarity to define sine, cosine, and tangent
Connections between similar triangles and trigonometry.
Learn how to label the sides of a right triangle as 'hypotenuse', 'opposite', and 'adjacent' in relation to one of the triangle's acute angles. Writing Trig Ratios
Writing the basic trig ratios given three side lengths; or given two side lengths. Writing Ratios part 1
Learn how to write the three primary trig. ratios for a right triangle given the three side lengths. Writing Ratios part 2
Learn how to write the three primary trig. ratios for a right triangle given two of the three side lengths. Finding a Side Using Trig
Using the tangent function to find an unknown side in a right triangle - two examples... one where the missing side ends up on the top of the ratio in the trig equation, and another where it ends up on the bottom. Finding an Angle Using Trig
Using the inverse tangent function to find an angle in a right. Trigonometric Ratios on a Calculator
Introduction to the trig function buttons (SIN,COS,TAN), and inverse function buttons (INVERSE SIN,COS,TAN) on a calculator.
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.