Sequence of Transformations
Examples, solutions, videos, and lessons to help High School students
when given a geometric figure and a rotation, reflection, or translation, draw
the transformed figure using, e.g., graph paper, tracing paper, or
geometry software. Specify a sequence of transformations that will
carry a given figure onto another.
Related Topics:
Common Core Geometry
Common Core Mathematics
Related Topics:
Common Core Geometry
Common Core Mathematics
Common Core: HSG-CO.A.5
Composite Transformation Theorems
There is a connection between the three transformations: reflections, translations and rotations.
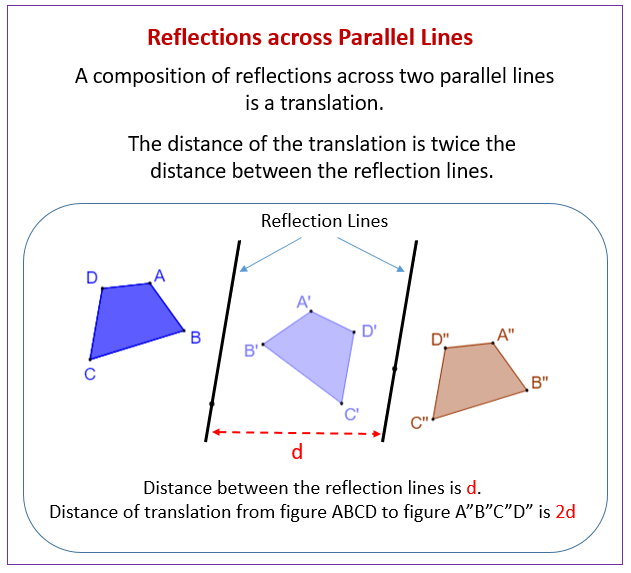
Parallel Lines Theorem: A composition of reflections across two parallel lines is a translation. When a figure is reflected in two parallel lines, the final image is a translation in the direction perpendicular to the parallel lines and twice the distance between them.
The following diagram shows that a composition of reflections across two parallel lines is a translation. Scroll down the page for more examples and solutions of reflections across parallel lines.
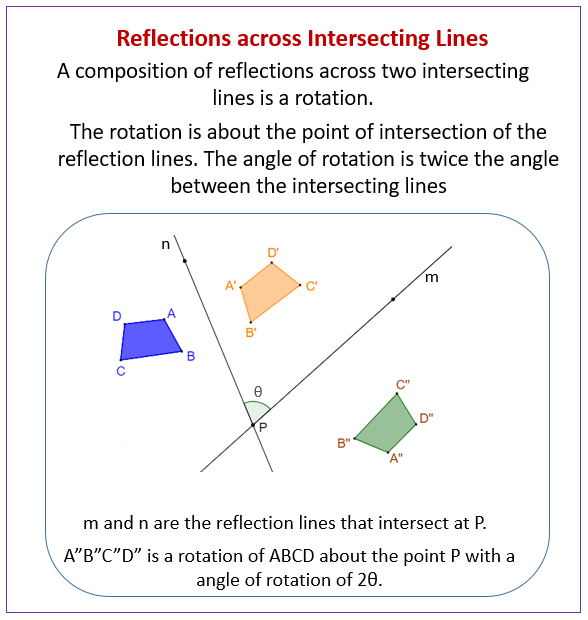
The following diagram shows that a composition of reflections across two intersecting lines is a rotation. Scroll down the page for more examples and solutions of reflections across intersecting lines.
Composition of Transformations (1)
Looking at composition of transformations - combining transformations in a series. Specifically looking at glide reflections: translation followed by reflection. Composition of Transformations (2)
Looking at composition of transformations - combining transformations in a series. Specifically looking at glide reflections, reflection followed by rotation. Composition of Transformations (3)
Composition Theorem: The composition of two or more isometries is an isometry.
Reflections in Parallel lines Theorem: If lines k and m are parallel then the reflection in line k followed by a reflection in line m is the same as a translation. Composition of Transformations (4)
Reflection in Intersecting lines Theorem: If lines k and m intersect at point, P, then a reflection in k followed by a reflection in m is the same as a rotation about the point, P.
Transformational Geometry (Translations, Rotations, Reflections) Defining transformations to match polygons Apply Composition of Transformations
Glide Reflection: Transformation followed by reflection
Translation followed by rotation
Composition of Transformations
Reflections in Parallel Lines Theorem
Reflections in Intersecting Lines Theorem
Composite Transformations in Geometric Figures
This video discusses composite transformations and work through some examples of how to do a composite transformation. Reflecting in Parallel Lines
Reflect the blue triangle in the blue-green line to form the green image. Reflect the green triangle in the green-red line to form the red image. The red triangle, being reflected twice, is oriented like the blue triangle.
Ignoring the green triangle, the result of the two reflections is to translate the blue triangle to the red triangle through twice the distance between the two mirror lines.
Reflecting in Intersecting Lines
Reflect the blue triangle in the blue-green line to form the green image. Reflect the green triangle in the green-red line to form the red image. The red triangle, being reflected twice, is oriented like the blue triangle.
Ignoring the green triangle, the result of the two reflections is to rotate the blue triangle to the red triangle about the intersection of the two mirror lines through twice the angle between them.
Composite Transformation Theorems
There is a connection between the three transformations: reflections, translations and rotations.
Parallel Lines Theorem: A composition of reflections across two parallel lines is a translation. When a figure is reflected in two parallel lines, the final image is a translation in the direction perpendicular to the parallel lines and twice the distance between them.
The following diagram shows that a composition of reflections across two parallel lines is a translation. Scroll down the page for more examples and solutions of reflections across parallel lines.
The following diagram shows that a composition of reflections across two intersecting lines is a rotation. Scroll down the page for more examples and solutions of reflections across intersecting lines.
Looking at composition of transformations - combining transformations in a series. Specifically looking at glide reflections: translation followed by reflection. Composition of Transformations (2)
Looking at composition of transformations - combining transformations in a series. Specifically looking at glide reflections, reflection followed by rotation. Composition of Transformations (3)
Composition Theorem: The composition of two or more isometries is an isometry.
Reflections in Parallel lines Theorem: If lines k and m are parallel then the reflection in line k followed by a reflection in line m is the same as a translation. Composition of Transformations (4)
Reflection in Intersecting lines Theorem: If lines k and m intersect at point, P, then a reflection in k followed by a reflection in m is the same as a rotation about the point, P.
Transformational Geometry (Translations, Rotations, Reflections) Defining transformations to match polygons Apply Composition of Transformations
Glide Reflection: Transformation followed by reflection
Translation followed by rotation
Composition of Transformations
Reflections in Parallel Lines Theorem
Reflections in Intersecting Lines Theorem
Composite Transformations in Geometric Figures
This video discusses composite transformations and work through some examples of how to do a composite transformation. Reflecting in Parallel Lines
Reflect the blue triangle in the blue-green line to form the green image. Reflect the green triangle in the green-red line to form the red image. The red triangle, being reflected twice, is oriented like the blue triangle.
Ignoring the green triangle, the result of the two reflections is to translate the blue triangle to the red triangle through twice the distance between the two mirror lines.
Reflecting in Parallel Lines from the Wolfram
Demonstrations Project by George Beck
Reflecting in Intersecting Lines
Reflect the blue triangle in the blue-green line to form the green image. Reflect the green triangle in the green-red line to form the red image. The red triangle, being reflected twice, is oriented like the blue triangle.
Ignoring the green triangle, the result of the two reflections is to rotate the blue triangle to the red triangle about the intersection of the two mirror lines through twice the angle between them.
Reflecting in Intersecting Lines from the Wolfram Demonstrations Project by George
Beck
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.