SAT Practice Test 4, Section 2: Questions 16 - 20

The following are worked solutions for the questions in the math sections of the SAT Practice Tests found in the Official SAT Study Guide.

It would be best that you go through the SAT practice test questions in the Study Guide first and then look at the worked solutions for the questions that you might need assistance in. Due to copyright issues, we are not able to reproduce the questions, but we hope that the worked solutions will be helpful.

Given:
A rectangle PQRS
Arcs QT and RT are quarter circle with centers at P and S, respectively
Radius of each quarter circle = 1

To find:
Area of shaded region

Solution:
Topic(s): Area of circle

Area of circle = πr²

Area of two quarter circles with radius 1 =

Area of rectangle = l w = 2 × 1 = 2

Shaded region = Area of rectangle –Area of two quarter circles =

Answer: (B)

17. Correct answer: (C)

Given:
The graph of y = f(x)

To find:
The graph of y = f(x + 2)

Solution:
We were given two points on the original graph (0, 1) and (1, 0).

To see how the points are translated:

For the point (0, 1),

let x + 2 = 0 ⇒ x = – 2. The new point is then (–2, 1)

For the point (1, 0),

let x + 2 = 1 ⇒ x = – 1. The new point is then (–1, 0)

The shape of the graph should be the same as the original except that it would be shifted two units to the left.

Answer: (C)

18. Correct answer: (B)

Given:
The figure
AB = BC
DE = EF = DF

To find:

Solution:
Topic(s): Types of triangles, pairs of angles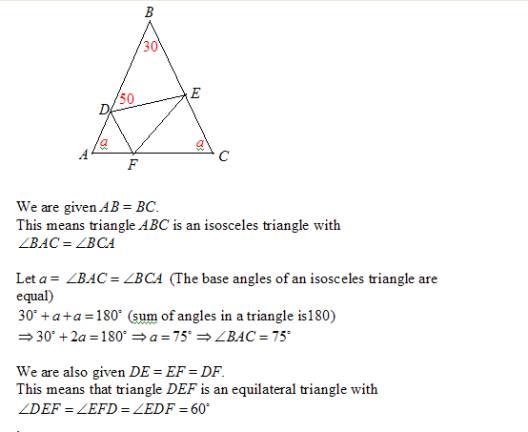

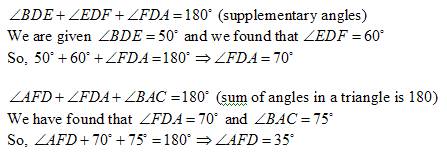
19. Correct answer: (A)

Given:
a, b, c and f are nonzero numbers

To find:
The proportion that is not equivalent

Solution:
Topic(s): Cross-multiply

Cross-multiply the fractions to find out which is the ones that is equivalent to the others

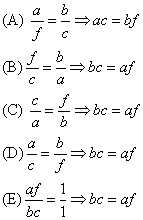
The proportion that is not equivalent to the others is (A)

Answer: (A)

20. Correct answer: (E)

Given:
x □ y = xy – y
a and b are positive integers

To find:
The expressions that can be equal to 0.

Solution:
We need to test the conditions. We factorize each expression and then determine what values of a or b would be necessary to get the expression equal to zero. If the values are positive integers then the expression can be equal to zero.

Condition I:

a □ b = ab – b = b(a – 1) = 0 ⇒ b = 0 or a = 1.

b cannot be 0 because we were told that it is a positive integer.

But, a can be 1. So, a □ b can be 0. ü

Condition II:

(a + b) □ b = (a + b) b – b = b(a + b – 1) = 0 ⇒ b = 0 or a+ b = 1

b cannot be 0 because we were told that it is a positive integer.

And a+ b cannot be 1 because the smallest values for a and b are 1. So, (a + b) □ b cannot be 0. û

Condition III:

a □ (a + b) = a (a + b) –(a + b) = (a – 1) (a + b) = 0 ⇒ a = 1 or a+ b = 0

a+ b cannot be 0 because the smallest values for a and b are 1.

But, a can be 1. So, a □ (a + b) can be 0 ü

Answer: (E) I and III

Custom Search