Ratios and Percents
More Lessons for Grade 6
A ratio is a comparison of any two quantities. It can be written as a to b, a: b or a/b.
In Grade 5, we explored the connections between fractions and decimals. Here, in grade 6, we will learn how to connect fractions and decimals with ratios and percents. We can name a number as a fraction, ratio, percent or decimal. For example, the fraction 5/10 can be written as the percent 50%, the decimal 0.50 or the ratio 5:10.
In this lesson, we will learn part-to-part ratio, part-to-total ratio, how to identify the different types of ratios, ratios and fractions, simplify ratios, equivalent ratios, ratios and percents.
Part-to-Part and Part-to-Whole Ratio
Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities. For example, The ratio of wings to beaks in the bird house at the zoo was 2:1, because for every 2 wings there was 1 beak. For every vote candidate A received, candidate C received nearly three votes.Example:
In a class, there are 11 boys and 14 girls. What is the ratio of the number of girls in the class to the number of pupils in the class?
Ratios and Fractions
How are fractions and ratios the same? How are they different? Is 3:5 the same as 3/5?Simplify Ratios
Eddie baked cookies with 4 cups of chocolate chips and 8 cups of sugar. What is the ratio of chocolate chips to sugar?Equivalent Ratios
Equivalent ratios are similar to equivalent fractions.How to tell if two ratios are equivalent by simplifying the fractions and by calculating the cross products? Find equivalent ratios using ratio tables.
Ratios and Percents
Percent is a ratio. Percent
should be viewed as a part-to-whole ratio that compares a number to a
whole divided into 100 equal parts.
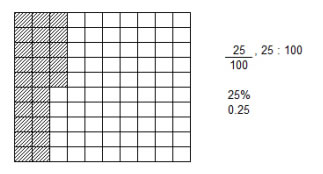
We can use a
hundredths grid to represent percents by
shading in the desired portion of the grid. E.g.,
to represent and model 25%, we could
use a hundredths grid to shade 25 blocks out of
100. This will help students to understand and
see the connection among fractions, decimals,
percents and ratios as 25 blocks shaded out of
100 could be seen as 25/100 or 1/4, 25:100 or 1:4, 0.25 or 25%
Susan correctly answered 21 out of 25 questions on her history quiz. On her science quiz she correctly answered 17 out of 20 questions. On which quiz did she do better?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.