Quadratic Functions
Related Pages
Quadratic Formula
Graphs Of Quadratic Functions
Factoring Out Common Factors
More Algebra Lessons
Math Worksheets
In these lessons, we will learn
- the different forms of quadratic functions (general, factored and vertex forms)
- how to convert from general form to factored form.
- how to convert from the general form to the vertex form using the vertex formula.
- how to convert from the general form to the vertex form using completing the square.
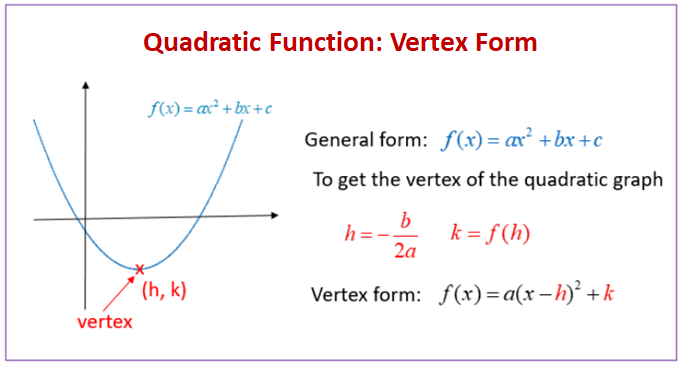
The following diagram shows how to use the vertex formula to convert a quadratic function from general form to vertex form. Scroll down the page for more examples and solutions for quadratic equations.
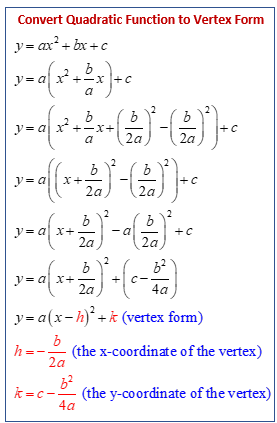
Algebra Worksheets
Practice your skills with the following Algebra worksheets:
Printable and Online Algebra Worksheets
Forms of Quadratic Functions
We can write quadratic functions in different ways or forms:
- General Form (Standard Form)
- Factored Form (Intercept Form)
- Vertex Form
-
General Form (Standard Form)
ax² + bx + c = 0, where a, b, and c are constants, and a ≠ 0.
For example, y = 2x2 + 5x − 30
Advantages:
This is the most common form, making it easy to identify the coefficients a, b, and c.
It’s the form used for applying the quadratic formula.
It’s useful for quickly determining the y-intercept (when x=0, y=c). -
Factored Form (Intercept Form):
a(x - r1)(x - r2) = 0, where a ≠ 0, and r1 and r2 are the roots (x-intercepts) of the equation.
For example, y = 2(x + 6)(x − 5).
Advantages:
It directly reveals the x-intercepts (which are also the roots when the function is zero) (r1 and r2). For example, the x-intercepts of y = 2(x + 6)(x − 5) are (−6, 0) and (5, 0)
It’s helpful for quickly sketching the graph of the quadratic function. -
Vertex Form:
a(x - h)² + k = 0, where a ≠ 0, and (h, k) represents the vertex of the parabola.
For example, y = 2(x + 6)2 − 5.
Advantages:
It directly reveals the vertex of the parabola, (h, k), which is the maximum or minimum point of the function. If a is positive then it is a minimum vertex. It a is negative then it is a maximum vertex.
It’s helpful for understanding the transformations of the basic quadratic function.
The following video looks at the various formats in which Quadratic Functions may be written as.
General Form to Factored Form
The following videos show how to change quadratic functions from general form to factored form.
General Form to Vertex Form by using the Vertex Formula
We can change a quadratic function from general form to vertex form by using the vertex formula.
Example of how to convert standard form to vertex form of a parabola equation.
General Form to Vertex Form by Completing the Square
We can change a quadratic function from general form to vertex form by completing the square.
The following videos show how to use the method of Completing the Square to convert a quadratic function from standard form to vertex form.
Key Features of Quadratic Equations
- Vertex:
The highest or lowest point on the parabola, depending on whether the parabola opens downward or upward.
Found using the vertex form or the formula h = −b/(2a), k = f(h). - Axis of Symmetry:
A vertical line that passes through the vertex, given by x = h x=h (from vertex form) or x = −b/(2a) (from standard form). - Roots (X-Intercepts):
The points where the parabola crosses the x-axis.
Found by solving f(x)=0. - Y-Intercept:
The point where the parabola crosses the y-axis.
Found by evaluating f(0).
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.