Prime Factorization Using Repeated Division

What Are Prime Factors

The prime factors of a number are the factors which are prime numbers. A prime number is a whole number greater than 1 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11).

What is Prime Factorization?
Prime factorization is the process of finding which prime numbers multiply together to make the original number. Essentially, you’re breaking down a composite number (a number with more than two factors) into its fundamental prime building blocks. The result is an expression showing the original number as a product of prime numbers.

Example:
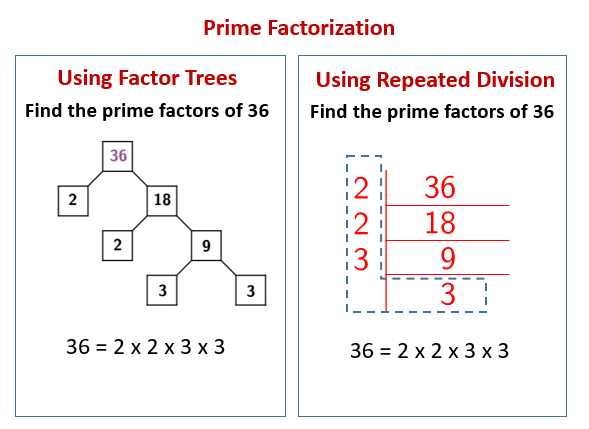
Find the prime factors of 36.
The prime factors of 36 are 2 and 3.
We can write 36 as a product of prime factors: 2 × 2 × 3 × 3

How to Find the Prime Factorization:
There are two common methods:

The following diagrams show Prime Factorization of a number using Factors Trees and using Repeated Division. Scroll down the page for more examples and solutions of prime factorization.

Factors & Multiples Worksheets
Practice your skills with the following factors worksheets:
Online & Printable Factors & Multiples Worksheets

1. Factor Tree Method:
   a. Start with the number you want to factorize as the root of the tree.
   b. Find any two factors of the number and branch out with these two factors.
   c. If a factor is prime, circle it (this branch is complete).
   d. If a factor is composite, continue to branch out by finding two of its factors.
   e. Repeat this process until all the “leaves” of the tree are prime numbers.
   f. The prime factorization is the product of all the circled prime numbers.
   

2. Division Method (or Upside-Down Division/Ladder Method/Stacked Division):
   a. Start with the number you want to factorize.
   b. Divide it by the smallest prime number (2, 3, 5, …).
   c. Write the prime number you divided by on the left and the quotient below the original number.
   d. Repeat the process with the quotient, again dividing by the smallest prime number.
   e. Continue this until the quotient becomes 1.
   f. The prime factors are all the prime numbers you used as divisors on the left side.
   

Key Points to Remember:

• You always divide by prime numbers.
• Start with the smallest prime number and work your way up.
• Every composite number has a unique prime factorization (Fundamental Theorem of Arithmetic).
• Prime factorization is useful for finding the Greatest Common Factor (GCF) and the Least Common Multiple (LCM) of numbers, simplifying fractions, and in cryptography.

Prime Factorization Using Stacked Division
Examples of how to use stacked division to find the prime factorization of a number rather than making a prime factorization tree.

Helpful Divisibility Rules
A number is divisible by 2 if it is even or ends in 0, 2, 4, 6, 8.
A number is divisible by 3 if the sum of the digits is divisible by 3.
A number is divisible by 5 if it ends in 0 or 5.

Example:
Use division to find the prime factorization.
a) 300
b) 693

• Show Video Lesson

Prime Factorization Using Stacked Division
Example:
Use division to find the prime factorization of 6,552.

• Show Video Lesson

Prime Factorization with Upside Down Division
Prime factors of a number can be found by using upside down division.

• Show Video Lesson

Prime Factorization with Upside Down Division
Example:
Find the prime factorization of the 210 by the division method.

• Show Video Lesson

Examples of prime factorization using repeated division
6, 24, 35, 51

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.