Partial Quotients Division Method
These lessons and examples help Grade 4 students learn about the partial quotients division method.
Related Pages
Long Division
Lessons and Worksheets for Common Core Grade 4 Math
Lessons for Grade 4 Math
How To Divide Using The Partial Quotients Method?
The partial quotients method (sometimes also called chunking) uses repeated subtraction to solve simple division questions.
When dividing a large number (dividend) by a small number (divisor).
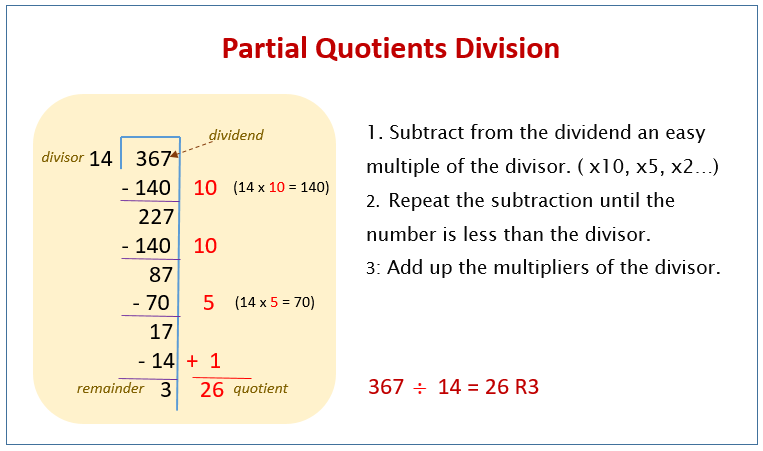
- Step 1: Subtract from the dividend an easy multiple (for example 100×, 10×, 5× 2×, etc.) of the divisor.
- Step 2: Repeat the subtraction until the large number has been reduced to zero or the remainder is less than the divisor.
- Step 3: Add up the multipliers of the divisor that were used in the repeated subtraction to find the answer of the division.
The following diagram shows how to divide using the partial quotient method. Scroll down the page for
more examples and solutions.
Lots of printable and online Division Worksheets to help you practice division.
Demonstration to help parents teach or assist in using partial quotients division at home
Example:
483 ÷ 13
Demonstration of the partial quotients division method
Examples:
185 ÷ 8
2185 ÷ 43
Everyday Math Partial Quotients Algorithm
Examples:
786 ÷ 5
How to divide numbers using the partial quotients algorithm?
Getting used to this method could help you mentally compute lots of real-world problems.
Examples:
78 ÷ 6
472 ÷ 4
739 ÷ 22
Everyday Math Partial Quotients Division Method With Whole Numbers
Example:
195 ÷ 12
Outline of partial quotients
Example:
381 ÷ 4
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.