Long Division
In these lessons, we will look at some examples of the long division of whole numbers.
Related Pages
Long Division
Division Worksheets
Worksheets: 3 digits ÷ 1 digit (without remainder)
Worksheets: 3 digits ÷ 1 digit (with remainder)
Lessons For Grade 4
More Numbers Lessons
In division, the number called the dividend is divided by the divisor, and the result is called quotient.
The following diagrams show the parts of a division: dividend, divisor, quotient, remainder. Scroll down the page for more examples and solutions long division.
Division Without Remainder
Example:
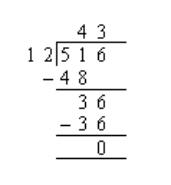
Solution:
Step 1: Start on the left. Check if first digit, 5, is
bigger than the divisor 12. Since 5 is not, we need to take the next digit as well.
51 divided by 12 gives 4 as the quotient since 12 × 4 = 48.
Write 4 above 1.
Step 2: Write the number 48 below 51. Subtract 48 from 51 to get a remainder of 3. Bring down the next digit, 6, and write it after 3.
Step 3: Now repeat from Step 1. 36 divided by 12, gives 3. Write 3 above 6. Write the number 36 below 36. Subtract 36 from 36 to get a remainder of 0.
Your answer is then 43.
Division With Remainder
Example:
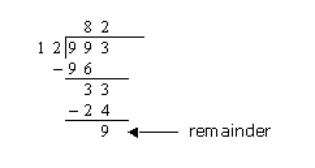
Solution:
Step 1: Start on the left. Check if first digit, 9, is bigger
than the divisor 12. Since 9 is not, we need to take the next digit as well.
99 divided by 12 gives 8 as the quotient since 12 × 8 = 96.
Write 8 above 9.
Step 2: Write the number 96 below 99. Subtract 96 from 99 to
get a remainder of 3. Bring down the next digit, 3, and write it after 3.
Step 3: Now repeat from Step 1. 33 divided by 12, gives 2. Write 2 above 3. Write the number 24 below 33. Subtract 24 from 33 to get a remainder of 9.
Your answer is then 82 remainder 9.
TAKE NOTE: For division, the divisor cannot be 0. For example, 23 ÷ 0 is not permissible.
Long Division with 1-Digit Divisors
Long Division with 2-Digit Divisors
| Check out our most popular games! | ||
|---|---|---|
 Fraction Concoction |
 Fact Family Game |
 Number Bond Garden |
 Online Addition Subtraction Game |
 Penguin Solitaire |
 Sawayama Solitaire |
 Ark Solitaire |
 Eldritch Invasion |
 Shenzhen Solitaire |
Check out more Solitaire games here.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.