One-Step Inequalities

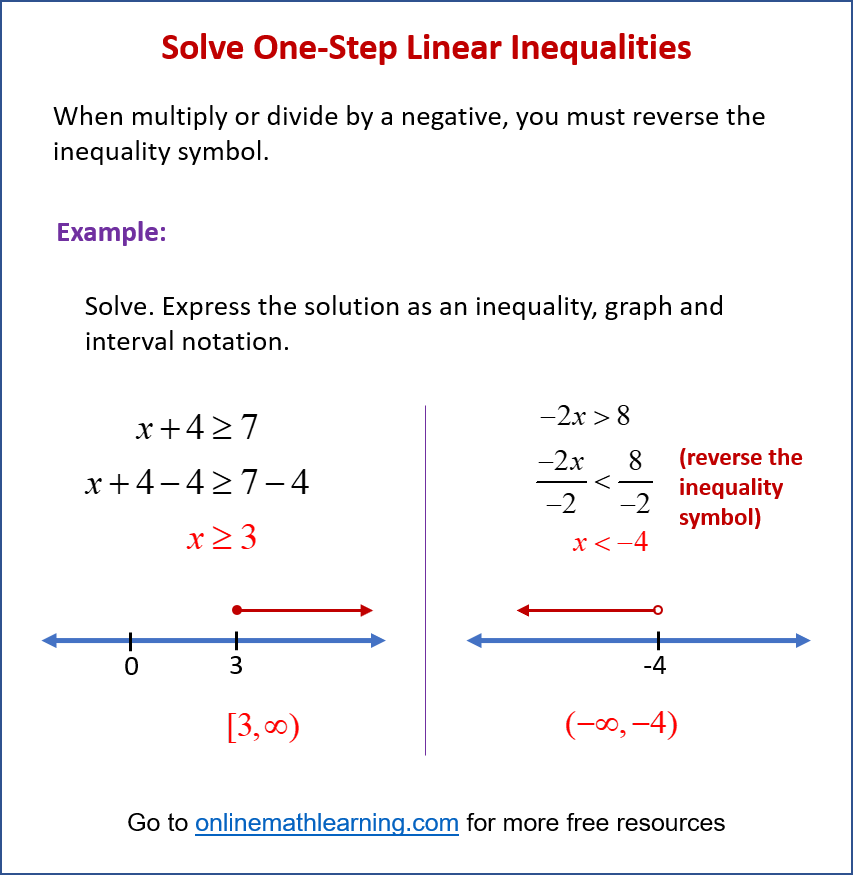
One-step linear inequalities are solved using addition, subtraction, multiplication, or division, similar to equations. However, there’s one critical rule:

When multiplying or dividing by a negative number, flip the inequality sign.

The inequality sign does not change when adding or subtracting.

The solutions to linear inequalities can be expressed in several ways: using inequalities, using a graph, or using interval notation.

The following diagrams give examples of solving a one-step linear inequalities. Scroll down the page for more examples and solutions.

Algebra Worksheets
Practice your skills with the following Algebra worksheets:
Printable & Online Algebra Worksheets

1. Addition and Subtraction
   Adding or subtracting the same number to both sides of an inequality does NOT change the direction of the inequality symbol.
   

Example 1: Using Addition
Solve: x − 7 < 10
Add 7 to both sides.
x − 7 + 7 < 10 + 7
Solution: x < 17

Example 2: Using Subtraction
Solve: y + 3 ≥ 5
Subtract 3 from both sides.
y + 3 − 3 ≥ 5 − 3
Solution: y ≥ 2

2. Multiplication and Division by a Positive Number
   Multiplying or dividing both sides of an inequality by a positive number does NOT change the direction of the inequality symbol.
   

Example 3: Multiplying by a Positive Number
Solve: \(\frac{w}{2} \le 4 \)
Multiply both sides by 2.
\(\frac{w}{2} × 2 ≤ 4 × 2 \)
Solution: w ≤ 8

Example 4: Dividing by a Positive Number
Solve: 5z > 20
Divide both sides by 5.
\(\frac{5z}{5} > \frac{20}{5} \)
Solution: z > 4

Multiplying/Dividing by a Negative Number
Multiplying or dividing both sides of an inequality by a negative number MUST reverse the direction of the inequality symbol.

Example 5: Multiplying by a Negative Number
Solve: \(\frac{a}{-3} < 6 \)
Multiply both sides by -3 (which is negative).
\(\frac{a}{-3} × (−3) > 6 × (−3) \) <– Remember to flip the symbol
Solution: a > −18

Example 6: Dividing by a Negative Number
Solve: −4b ≤ 12
Divide both sides by -4 (which is negative).
\(\frac{-4b}{-4} × (−4) ≥ 12 ×(−4) \) <– Remember to flip the symbol
Solution: b ≥ −3

One-Step Inequalities

• Show Step-by-step Solutions

One-Step Inequalities 2

• Show Step-by-step Solutions

One-step Inequality Examples

• Show Step-by-step Solutions

Solving one-step inequalities

• Show Step-by-step Solutions

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.