Mutually Exclusive Events

Mutually Exclusive Events
In probability, mutually exclusive events (also called disjoint events) are events that cannot happen at the same time. If one event occurs, the other cannot. They have no outcomes in common.

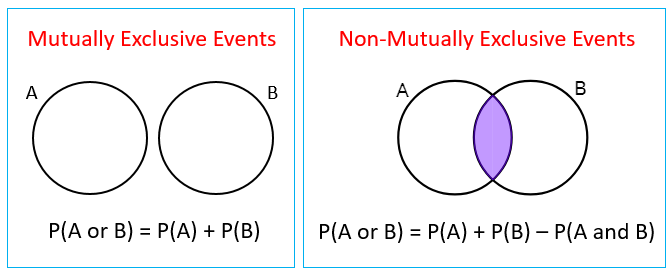
The following diagrams show the formulas for the probability of mutually exclusive events and non-mutually exclusive events. Scroll down the page for examples and solutions.

Probability Worksheets
Practice your skills with the following worksheets:
Printable & Online Probability Worksheets

Probability Of Mutually Exclusive Events

Two events are said to be mutually exclusive if they cannot happen at the same time.

For example, if we toss a coin, either heads or tails might turn up, but not heads and tails at the same time. Similarly, in a single throw of a die, we can only have one number shown at the top face. The numbers on the face are mutually exclusive events.

If A and B are mutually exclusive events then the probability of A happening OR the probability of B happening is P(A) + P(B).

P(A or B) = P(A) + P(B)

Example:
The probabilities of three teams A, B and C winning a badminton competition are 1/3, 1/5 and 1/9 respectively.

Calculate the probability that
a) either A or B will win
b) either A or B or C will win
c) none of these teams will win
d) neither A nor B will win

Solution:

c) P(none will win) = 1 – P(A or B or C will win)

d) P(neither A nor B will win) = 1 – P(either A or B will win)

Mutually Exclusive Events

Probabilities of Mutually Exclusive Events
If two events are ‘mutually exclusive’ they cannot occur at the same time.

Learn all about mutually exclusive events in this video.
For mutually exclusive events the total probabilities must add up to 1.

Probability - P(A ∪ B) and Mutually Exclusive Events
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
For mutually exclusive events, P(A ∩ B) = 0.

• Show Video Lesson

Mutually Exclusive Events And Non-Mutually Exclusive Events

The following video shows how to calculate the probability of mutually exclusive events and non-mutually exclusive events.

Examples:

1. Find the probability of drawing a yellow ball or drawing a three.
2. Find the probability of drawing a red ball or drawing an odd number ball.

• Show Video Lesson

Mutually Exclusive Events - Introduction

Examples:

1. What is the probability of drawing a heart and a black card?
2. What is the probability of drawing a heart or a black card?
3. What is the probability of drawing a heart and a face card?
4. What is the probability of drawing a heart or a face card?

• Show Video Lesson

Mutually Exclusive Events Vs Independent Events

Example:
The figure shows how 25 people travelled to work: B for bicycle, T for Train and W for Walk.
a) Write down two of these events that are mutually exclusive. Give a reason for your answer.
b) Determine whether or not B and T are independent events.

• Show Video Lesson

Independence And Mutually Exclusive

Mutually exclusive events cannot be independent events.
Independent events cannot be mutually exclusive events.

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.