Multiplying Algebraic Expressions
Related Pages
Algebraic Expressions
Adding And Subtracting Algebraic Expressions
More Algebra Lessons
In these lessons, we will learn how to multiply algebraic expressions.
Multiplying algebraic expressions involves using the distributive property and the rules of exponents. Then, combine like terms to simplify the result.
The following diagram shows how to multiply algebraic expressions. Scroll down the page for more examples and solutions on how to multiply expressions.
The following diagram shows some expansions, that are useful to remember, when multiplying two algebraic expressions or binomials. Scroll down the page for more examples and solutions on how to expand expressions.
Algebra Math Worksheets
Practice your skills with the following worksheets:
Printable & Online Algebra Worksheets
How to Multiply a Term and an Algebraic Expression?
We will first consider examples of multiplying a term and an algebraic expression.
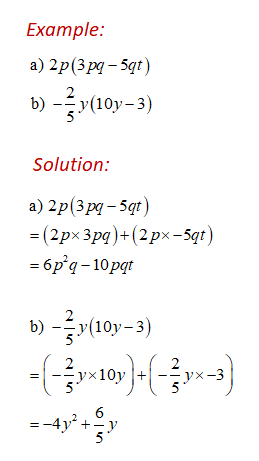
How to Multiply Two Algebraic Expressions?
Next, we will also consider the multiplication of two algebraic expressions: (a + b)(c + d)
Such an operation is called ‘expanding the expression’.
To expand the expression, we multiply each term in the first pair of brackets by every term in
the second pair of brackets.
Example:
Expand the following:
a) (y – 3)(2y + 5)
b) (a + b)2
Solution:
a) (y – 3)(2y + 5)
= y(2y+ 5) – 3(2y + 5)
= (y × 2y) + (y × 5) + (–3 × 2y) + (–3 × 5)
= 2y2 + 5y – 6y – 15
= 2y2 – y – 15
b) (a + b)2
= (a + b)(a + b) = a(a + b) + b(a + b)
= a2 + ab + ab + b2
= a2 + 2ab + b2
Multiplication of Algebraic Expressions:
- Multiply the numbers (numerical coefficients)
- Multiply the letters (literal numbers) - Exponents can only be combined if the base is the same.
Example:
- -2c2(-7c3x5)(bx2)2 =
- 3a2(-ab4)(2a2c3) =
- 3sy(s - t) =
- 4uv2(3u2z - 7u3) =
Examples of multiplying expressions using the distributive property
Example:
- (x + 2)(x + 3)
- (5x + 9)(4x - 2)
- (2x + y)(3x + 2y)
- (2x + 2)2
Multiplication of Algebraic Expressions - Use the distributive property
Example:
- 3cy2(-4cx - 2xy3)
- (x + 5)(x -2)
Multiplication of Algebraic Expressions - Solving Complex Questions
Example:
- (b + 3c)2
- (2y - 4)3
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.