

The Mean as a Balance Point
Related Topics:
Lesson Plans and Worksheets for Grade 6
Lesson Plans and Worksheets for all Grades
More Lessons for Grade 6
Common Core For Grade 6
Videos and solutions to help grade 6 students learn how to characterize the center of a distribution by its mean in the sense of a balance point and that the mean is the value such that the sum of the deviations is equal to zero.
Lesson 7 Student Outcomes
• Students characterize the center of a distribution by its mean in the sense of a balance point.
• Students understand that the mean is a balance point by calculating the distances of the data points from the mean and call the distances, deviations.
• Students understand that the mean is the value such that the sum of the deviations is equal to zero.
Lesson 7 Summary
In this lesson, the “balance” process was developed to provide another way in which the mean characterizes the “center” of a distribution.
• The mean is the balance point of the data set when the data are shown as dots on a dot plot (or pennies on a ruler).
• The difference formed by subtracting the mean from a data point is called its deviation.
• The mean can be defined as the value that makes the sum of all deviations in a distribution equal to zero.
• The mean is the point that balances the sum of the positive deviations with the sum of the negative deviations.
The following figures show the Mean as a Balance Point. Scroll down the page for examples and solutions.
Lesson 7 Classwork
In Lesson 3, Robert gave us an informal interpretation of the center of a data set. In Lesson 6, Michelle developed a more formal interpretation of the center as a “fair share” mean, a value that every person in the data set would have if they all had the same value. In this lesson, Sabina will show us how to interpret the mean as a “balance point.”
Example 1: The Mean as a Balance Point
Sabina wants to know how long it takes students to get to school. She asks two students how long it takes them to get to school. It takes one student 1 minute and the other student 11 minutes. Sabina represents these data on a ruler putting a penny at 1 and another at 11 and shows that the ruler balances on the eraser end of a pencil at 6. Note that the mean of 1 and 11 is also 6. Sabina thinks that there might be a connection between the mean of two data points and where they balance on a ruler. She thinks the mean may be the balancing point. What do you think? Will Sabina’s ruler balance at 6? Is the mean of 1 and 11 equal to 6? Sabina shows the result on a dot plot.
Sabina decides to move the penny at 1 to 4 and the other penny from 11 to 8 on the ruler, noting that the movement for the two pennies is the same distance but in opposite directions. She notices that the ruler still balances at 6. Sabina decides that if data points move the same distance but in opposite directions, the balancing point on the ruler does not change. Does this make sense? Notice that this implies that the mean of the time to get to school for two students who take 4 minutes and 8 minutes to get to school is also 6 minutes.
Sabina continues by moving the penny at 4 to 6. To keep the ruler balanced at 6, how far should Sabina move the penny at 8 and in what direction? Since the penny at 4 moved two to the right, to maintain the balance the penny at 8 needs to move two to the left. Both pennies are now at 6, and the ruler clearly balances there. Note that the mean of these two values (6 minutes and 6 minutes) is still 6 minutes.
Exercises 1–2
Now it is your turn to try balancing two pennies on a ruler.
1. Tape one penny at 2.5 on your ruler.
a. Where should a second penny be taped so that the ruler will balance at 6?
b. How far is the penny at 2.5 from 6? How far is the other penny from 6?
c. Is the mean of the two locations of the pennies equal to 6?
2. Move the penny that is at 2.5 two inches to the right.
a. Where will the point be placed?
b. What do you have to do with the other data point to keep the balance point at 6?
c. What is the mean of the two new data points? Is it the same value as the balancing point of the ruler?
Example 2: Understanding Deviations
In the above example using two pennies, it appears that the balance point of the ruler occurs at the mean location of the two pennies. We computed the distance from the balance point to each penny location and treated the distances as positive numbers. In statistics, we calculate a difference by subtracting the mean from the data point and call it the deviation of a data point from the mean. So, points to the left of the mean are less than the mean and have a negative deviation. Points to the right of the mean are greater than the mean and have a positive deviation.
Let’s look at Sabina’s initial placement of pennies at 1 and 11 with a mean at on the graph below. Notice that the deviations are +5 and -5. What is the sum of the deviations?
Similarly, when Sabina moved the pennies to 4 and 8, the deviation of 4 from 6 is 4 - 6 = -2, and the deviation of 8 from 6 is 8 - 6 = 2. Here again, the sum of the two deviations is 0, since It appears that for two data points the mean is the point when the sum of its deviations is equal to 0.
Exercises 3–4
Refer back to Exercise 2, where one penny was located at and the mean was at 6.
3. Where was the second penny located?
4. Calculate the deviations of the two pennies and show that the sum of the deviations is 0.
Example 3: Balancing the Mean
Sabina wants to know what happens if there are more than two data points. Suppose there are three students. One student lives 2 minutes from school, and another student lives 9 minutes from school. If the mean time for all three students is 6 minutes, she wonders how long it takes the third student to get to school. She tapes pennies at 2 and 9 and by experimenting finds the ruler balances with a third penny placed at 7. To check what she found, she calculates deviations.
The data point at 2 has a deviation of -4 from the mean. The data point at 7 has a deviation of +1 from the mean. The data point at 9 has a deviation of +3 from the mean. The sum of the three deviations is 0, since -4 + 1 + 3. So, the mean is indeed 6 minutes.
Robert says that he found out that the third penny needs to be at 7 without using his ruler. He put 2 and 9 on a dot plot. He says that the sum of the two deviations for the points at 2 and 9 is -1, since -4 + 3 = -1. So, he claims that the third data point would require a deviation of +1 to make the sum of all three deviations equal to 0. That makes the third data point 1 minute above the mean of 6 minutes, which is 7 minutes.
Exercises 5–7
Imagine you are balancing pennies on a ruler.
5. Suppose you place one penny each at 3, 7, and 8 on your ruler.
a. Sketch a picture of the ruler. At what value do you think the ruler will balance? Mark the balancing point with the symbol △.
b. What is the mean of 3, 7, and 8? Does your ruler balance at the mean?
c. Show part (a) on a dot plot. Mark the balancing point with the symbol △.
d. What are the deviations from each of the data points to the balancing point? What is the sum of the deviations? What is the value of the mean?
6. Now suppose you place a penny each at and on your ruler.
a. Draw a dot plot representing these two pennies.
b. Estimate where to place a third penny on your ruler so that the dot plot above. Mark the balancing point with the symbol △.
c. Explain why your answer in part (b) is true by calculating the deviations of the points from 6. Is the sum of the deviations equal 0?
7. Suppose you place two pennies at 7 and one penny at 9 on your ruler.
a. Draw a dot plot representing these three pennies.
b. Estimate where to place a fourth penny on your ruler so that the ruler balances at 6 and mark the point on the dot plot above. Mark the balancing point with the symbol △.
c. Explain why your answer in part (b) is true by calculating the deviations of the points from 6. Does the sum of the deviations equal 0?
Example 4: Finding the Mean
Not all data distributions on a ruler are going to have a “fair share” mean, or “balance point” of . What if the data were 1, 3, and 8? Will your ruler balance at 6? Why not?
Notice that the deviation of 1 from 6 is -5. The deviation of 3 from 6 is -3. The deviation of 8 from 6 is +2. The sum of the deviations is -6 since -5 + (-3) + 2 = -6. The sum should be 0. Therefore, the mean is not at 6. Is the mean greater than 6 or less than 6? The sum of the deviations is negative. To decrease the negative deviations and increase the positive deviations, the balance point would have to be less than 6.
Let’s see if the balance point is at 5. The deviation of 1 from 5 is -4. The deviation of 3 from 5 is -2. The deviation of 8 from 5 is +3. The sum of the three deviations is -3, since -4 + (-2) + 3 = -3. That’s closer to 0 than before. Let’s keep going and try 4 as the balance point. The deviation of 1 from 4 is -3. The deviation of 3 from 4 is -1. The deviation of 8 from 4 is +4. The sum of the deviations is 0, since -3 + (-1) + 4 = 0. The balancing point of the data distribution of 1, 3, and 8 shown on your ruler or on a dot plot is at 4. The mean of 1, 3, and 8 is 4.
Exercise 8
Use what you have learned about the mean to answer the following questions.
8. Recall in Lesson 6 that Michelle asked ten of her classmates for the number of hours they usually sleep when there is school the next day. Their responses (in hours) were 8, 10, 8, 8, 11, 11, 9, 8, 10, 7.
a. It’s hard to balance ten pennies. Instead of actually using pennies and a ruler, draw a dot plot that represents the data set.
b. Use your dot plot to find the balance point. What is the sum of the deviations of the data points from the fair share mean of 9 hours?
Problem Set
1. The number of pockets in the clothes worn by four students to school today is 4, 1, 3, 4.
a. Perform the fair share process to find the mean number of pockets for these four students. Sketch the cubes representations for each step of the process.
b. Find the total of the distances on each side of the mean to show the mean found in part (a) is correct.
2. The times (rounded to the nearest minute) it took each of six classmates to run a mile are 7, 9, 10, 11, 11, and 12 minutes.
a. Draw a dot plot representation for the mile times.
b. Suppose that Sabina thinks the mean is 11 minutes. Is she correct? Explain your answer.
c. What is the mean?
3. The prices per gallon of gasoline (in cents) at five stations across town on one day are shown in the following dot plot. The price for a sixth station is missing, but the mean price for all six stations was reported to be 380 cents per gallon. Use the balancing process to determine the price of a gallon of gasoline at the sixth station.
4. The number of phones (landline and cell) owned by the members of each of nine families is 3,5,6,6,6,6,7,7,8.
a. Use the mathematical formula for the mean (determine the sum of the data points, and divide by the number of data points) to find the mean number of phones owned for these nine families.
b. Draw a dot plot of the data, and verify your answer in part (a) by using the balancing process.


Lesson Plans and Worksheets for Grade 6
Lesson Plans and Worksheets for all Grades
More Lessons for Grade 6
Common Core For Grade 6
Videos and solutions to help grade 6 students learn how to characterize the center of a distribution by its mean in the sense of a balance point and that the mean is the value such that the sum of the deviations is equal to zero.
New York State Common Core Math Grade 6, Module 6, Lesson 7
Download lessons for 6th GradeLesson 7 Student Outcomes
• Students characterize the center of a distribution by its mean in the sense of a balance point.
• Students understand that the mean is a balance point by calculating the distances of the data points from the mean and call the distances, deviations.
• Students understand that the mean is the value such that the sum of the deviations is equal to zero.
Lesson 7 Summary
In this lesson, the “balance” process was developed to provide another way in which the mean characterizes the “center” of a distribution.
• The mean is the balance point of the data set when the data are shown as dots on a dot plot (or pennies on a ruler).
• The difference formed by subtracting the mean from a data point is called its deviation.
• The mean can be defined as the value that makes the sum of all deviations in a distribution equal to zero.
• The mean is the point that balances the sum of the positive deviations with the sum of the negative deviations.
The following figures show the Mean as a Balance Point. Scroll down the page for examples and solutions.
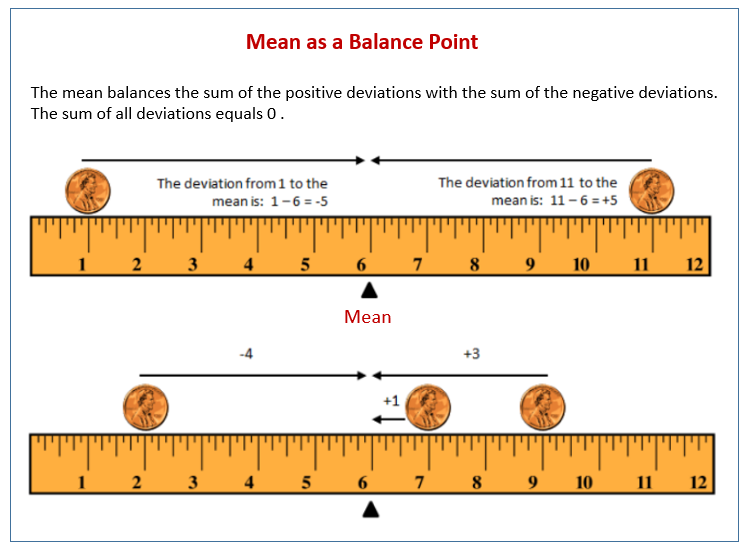
In Lesson 3, Robert gave us an informal interpretation of the center of a data set. In Lesson 6, Michelle developed a more formal interpretation of the center as a “fair share” mean, a value that every person in the data set would have if they all had the same value. In this lesson, Sabina will show us how to interpret the mean as a “balance point.”
Example 1: The Mean as a Balance Point
Sabina wants to know how long it takes students to get to school. She asks two students how long it takes them to get to school. It takes one student 1 minute and the other student 11 minutes. Sabina represents these data on a ruler putting a penny at 1 and another at 11 and shows that the ruler balances on the eraser end of a pencil at 6. Note that the mean of 1 and 11 is also 6. Sabina thinks that there might be a connection between the mean of two data points and where they balance on a ruler. She thinks the mean may be the balancing point. What do you think? Will Sabina’s ruler balance at 6? Is the mean of 1 and 11 equal to 6? Sabina shows the result on a dot plot.
Sabina decides to move the penny at 1 to 4 and the other penny from 11 to 8 on the ruler, noting that the movement for the two pennies is the same distance but in opposite directions. She notices that the ruler still balances at 6. Sabina decides that if data points move the same distance but in opposite directions, the balancing point on the ruler does not change. Does this make sense? Notice that this implies that the mean of the time to get to school for two students who take 4 minutes and 8 minutes to get to school is also 6 minutes.
Sabina continues by moving the penny at 4 to 6. To keep the ruler balanced at 6, how far should Sabina move the penny at 8 and in what direction? Since the penny at 4 moved two to the right, to maintain the balance the penny at 8 needs to move two to the left. Both pennies are now at 6, and the ruler clearly balances there. Note that the mean of these two values (6 minutes and 6 minutes) is still 6 minutes.
Exercises 1–2
Now it is your turn to try balancing two pennies on a ruler.
1. Tape one penny at 2.5 on your ruler.
a. Where should a second penny be taped so that the ruler will balance at 6?
b. How far is the penny at 2.5 from 6? How far is the other penny from 6?
c. Is the mean of the two locations of the pennies equal to 6?
2. Move the penny that is at 2.5 two inches to the right.
a. Where will the point be placed?
b. What do you have to do with the other data point to keep the balance point at 6?
c. What is the mean of the two new data points? Is it the same value as the balancing point of the ruler?
Example 2: Understanding Deviations
In the above example using two pennies, it appears that the balance point of the ruler occurs at the mean location of the two pennies. We computed the distance from the balance point to each penny location and treated the distances as positive numbers. In statistics, we calculate a difference by subtracting the mean from the data point and call it the deviation of a data point from the mean. So, points to the left of the mean are less than the mean and have a negative deviation. Points to the right of the mean are greater than the mean and have a positive deviation.
Let’s look at Sabina’s initial placement of pennies at 1 and 11 with a mean at on the graph below. Notice that the deviations are +5 and -5. What is the sum of the deviations?
Similarly, when Sabina moved the pennies to 4 and 8, the deviation of 4 from 6 is 4 - 6 = -2, and the deviation of 8 from 6 is 8 - 6 = 2. Here again, the sum of the two deviations is 0, since It appears that for two data points the mean is the point when the sum of its deviations is equal to 0.
Exercises 3–4
Refer back to Exercise 2, where one penny was located at and the mean was at 6.
3. Where was the second penny located?
4. Calculate the deviations of the two pennies and show that the sum of the deviations is 0.
Example 3: Balancing the Mean
Sabina wants to know what happens if there are more than two data points. Suppose there are three students. One student lives 2 minutes from school, and another student lives 9 minutes from school. If the mean time for all three students is 6 minutes, she wonders how long it takes the third student to get to school. She tapes pennies at 2 and 9 and by experimenting finds the ruler balances with a third penny placed at 7. To check what she found, she calculates deviations.
The data point at 2 has a deviation of -4 from the mean. The data point at 7 has a deviation of +1 from the mean. The data point at 9 has a deviation of +3 from the mean. The sum of the three deviations is 0, since -4 + 1 + 3. So, the mean is indeed 6 minutes.
Robert says that he found out that the third penny needs to be at 7 without using his ruler. He put 2 and 9 on a dot plot. He says that the sum of the two deviations for the points at 2 and 9 is -1, since -4 + 3 = -1. So, he claims that the third data point would require a deviation of +1 to make the sum of all three deviations equal to 0. That makes the third data point 1 minute above the mean of 6 minutes, which is 7 minutes.
Exercises 5–7
Imagine you are balancing pennies on a ruler.
5. Suppose you place one penny each at 3, 7, and 8 on your ruler.
a. Sketch a picture of the ruler. At what value do you think the ruler will balance? Mark the balancing point with the symbol △.
b. What is the mean of 3, 7, and 8? Does your ruler balance at the mean?
c. Show part (a) on a dot plot. Mark the balancing point with the symbol △.
d. What are the deviations from each of the data points to the balancing point? What is the sum of the deviations? What is the value of the mean?
6. Now suppose you place a penny each at and on your ruler.
a. Draw a dot plot representing these two pennies.
b. Estimate where to place a third penny on your ruler so that the dot plot above. Mark the balancing point with the symbol △.
c. Explain why your answer in part (b) is true by calculating the deviations of the points from 6. Is the sum of the deviations equal 0?
7. Suppose you place two pennies at 7 and one penny at 9 on your ruler.
a. Draw a dot plot representing these three pennies.
b. Estimate where to place a fourth penny on your ruler so that the ruler balances at 6 and mark the point on the dot plot above. Mark the balancing point with the symbol △.
c. Explain why your answer in part (b) is true by calculating the deviations of the points from 6. Does the sum of the deviations equal 0?
Example 4: Finding the Mean
Not all data distributions on a ruler are going to have a “fair share” mean, or “balance point” of . What if the data were 1, 3, and 8? Will your ruler balance at 6? Why not?
Notice that the deviation of 1 from 6 is -5. The deviation of 3 from 6 is -3. The deviation of 8 from 6 is +2. The sum of the deviations is -6 since -5 + (-3) + 2 = -6. The sum should be 0. Therefore, the mean is not at 6. Is the mean greater than 6 or less than 6? The sum of the deviations is negative. To decrease the negative deviations and increase the positive deviations, the balance point would have to be less than 6.
Let’s see if the balance point is at 5. The deviation of 1 from 5 is -4. The deviation of 3 from 5 is -2. The deviation of 8 from 5 is +3. The sum of the three deviations is -3, since -4 + (-2) + 3 = -3. That’s closer to 0 than before. Let’s keep going and try 4 as the balance point. The deviation of 1 from 4 is -3. The deviation of 3 from 4 is -1. The deviation of 8 from 4 is +4. The sum of the deviations is 0, since -3 + (-1) + 4 = 0. The balancing point of the data distribution of 1, 3, and 8 shown on your ruler or on a dot plot is at 4. The mean of 1, 3, and 8 is 4.
Exercise 8
Use what you have learned about the mean to answer the following questions.
8. Recall in Lesson 6 that Michelle asked ten of her classmates for the number of hours they usually sleep when there is school the next day. Their responses (in hours) were 8, 10, 8, 8, 11, 11, 9, 8, 10, 7.
a. It’s hard to balance ten pennies. Instead of actually using pennies and a ruler, draw a dot plot that represents the data set.
b. Use your dot plot to find the balance point. What is the sum of the deviations of the data points from the fair share mean of 9 hours?
Problem Set
1. The number of pockets in the clothes worn by four students to school today is 4, 1, 3, 4.
a. Perform the fair share process to find the mean number of pockets for these four students. Sketch the cubes representations for each step of the process.
b. Find the total of the distances on each side of the mean to show the mean found in part (a) is correct.
2. The times (rounded to the nearest minute) it took each of six classmates to run a mile are 7, 9, 10, 11, 11, and 12 minutes.
a. Draw a dot plot representation for the mile times.
b. Suppose that Sabina thinks the mean is 11 minutes. Is she correct? Explain your answer.
c. What is the mean?
3. The prices per gallon of gasoline (in cents) at five stations across town on one day are shown in the following dot plot. The price for a sixth station is missing, but the mean price for all six stations was reported to be 380 cents per gallon. Use the balancing process to determine the price of a gallon of gasoline at the sixth station.
4. The number of phones (landline and cell) owned by the members of each of nine families is 3,5,6,6,6,6,7,7,8.
a. Use the mathematical formula for the mean (determine the sum of the data points, and divide by the number of data points) to find the mean number of phones owned for these nine families.
b. Draw a dot plot of the data, and verify your answer in part (a) by using the balancing process.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.