Solve Linear Inequalities with Fractions

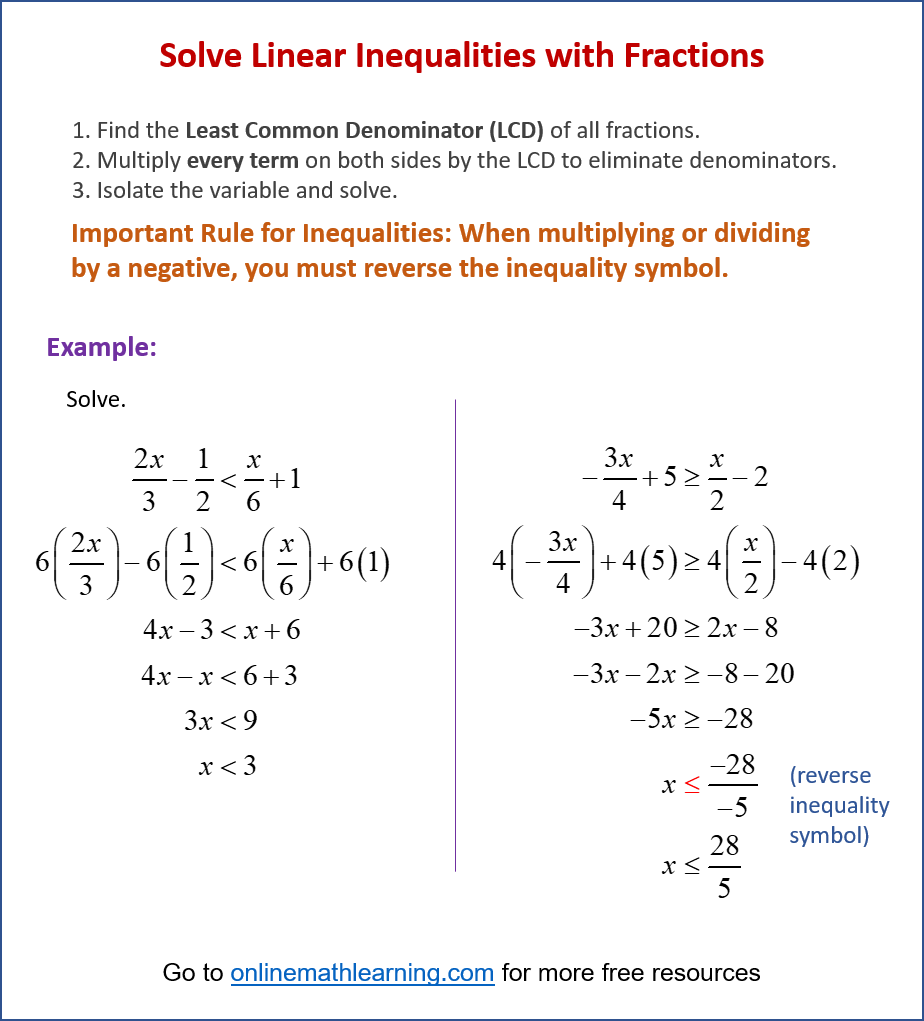
Solving linear inequalities with fractions follows the same core principles as solving linear inequalities without them, but with an added initial step that can make the process much easier: clearing the denominators by multiplying with the least common denominator (LCD).

The Rule of Inequalities still applies:
When you multiply or divide both sides of an inequality by a negative number, you must reverse (flip) the direction of the inequality symbol.

The following figure shows how to solve linear inequalities with fractions. Scroll down the page for more examples and solutions.

Algebra Worksheets
Practice your skills with the following Algebra worksheets:
Printable & Online Algebra Worksheets

Steps to Solve Linear Inequalities with Fractions:

1. Find the Least Common Denominator (LCD): Determine the LCD of all the fractions in the inequality.
2. Clear the Denominators: Multiply every single term on both sides of the inequality by the LCD. This will eliminate all the denominators, leaving you with an inequality involving only integers.
3. Solve as a Multi-Step Inequality: Once the denominators are cleared, proceed with the standard steps for solving multi-step linear inequalities:

• Distribute if there are parentheses.
• Combine like terms on each side.
• Move all variable terms to one side and all constant terms to the other.
• Isolate the variable by dividing or multiplying. REMEMBER to flip the inequality sign if you multiply or divide by a negative number!

4. Simplify: Express your answer in its simplest form.

Solving Single-Step Inequalities by taking the Reciprocal
Example:
-5/2 x ≤ -1/5

• Show Step-by-step Solutions

Solving Two - Step Linear Inequalities
Examples:
Solve each of the following:
a) 4x - 6 > 1
b) -x/8 + 8 ≥ 14
c) (x + 6)/11 < 2

• Show Step-by-step Solutions

Solving a two-step linear inequality with fractions
Example:
2/3 > -4y - 8 1/3

• Show Step-by-step Solutions

How to Solve a two-step linear inequality with a fractional coefficient?
Examples:

1. Solve the inequality for u.
   -8 < -6u/5 + 8
   Simplify your answer as much as possible.
   
   
2. Solve the inequality for w.
   -4 ≤ 3 - 7/8 w
   Simplify your answer as much as possible.
   

• Show Step-by-step Solutions

Solving Inequalities With Fractions
When solving inequalities with fractions, remember that inequality means that there is a “less than” or “greater than” part to the question. Look for common denominators when solving inequalities with fractions
Example:
2/3 + 1/3 < 2/3

• Show Step-by-step Solutions

How to Solve Inequalities that contain Fractions?
Learn to solve inequalities that contain fractions.
Example:
Solve
-11x/5 + 7/15 ≤ 9/2

• Show Step-by-step Solutions

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.