Intersecting Secants Theorem
Related Pages
More Lessons for High School Regents Exam
Math Worksheets
These lessons cover High School Math based on the topics required for the Regents Exam conducted by NYSED.
How to find segment lengths using the Segments of Secants Theorem (Intersecting Secant Theorem) and Segments of Secants and Tangents Theorem?
What is a secant?
A secant is a line that crosses a circle in two places.
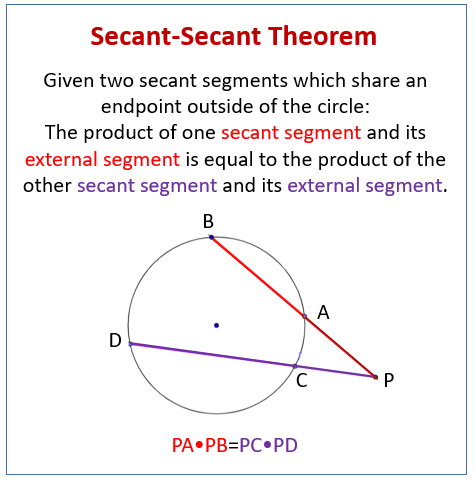
What is the Intersecting Secant Theorem or Segments of Secants Theorem?
If two secant segments are drawn to a circle from the same external point, the product of the length of one secant segment and its external part is equal to the product of the length of the other secant segment and its external part.
For example, in the following diagram PA × PD = PC × PB
The following diagram shows the Secant-Secant Theorem. Scroll down the page for more examples and solutions on how to use the Secant-Secant Theorem.
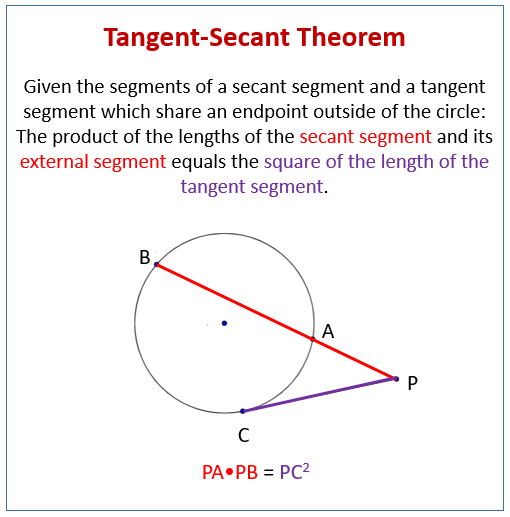
What is the Segments of Secants and Tangents Theorem?
If a secant segment and a tangent segment share the same endpoint outside the circle, then the product of the lengths of one secant and its external segment equals the square of the length of the tangent segment.
The following diagram shows the Tangent-Secant Theorem. Scroll down the page for more examples and solutions on how to use the Tangent-Secant Theorem.
This following videos explain the Segments of Secants Theorem and Segments of Secants and Tangents Theorem and how to find segment lengths using the theorems.
Segments of Secants Theorem and Segments of Secants and Tangents Theorem
Segments of Secants Theorem
Two secant segments which share an endpoint outside of the circle. The product of one secant segment and its external segment is equal to the product of the other secant segment and its external segment.
Errata: For the example 2, the answer should be x = 9.
Segments of Secants and Tangents Theorem
The segments of a secant segment and a tangent segment which share an endpoint outside of the circle. The product of the lengths of the secant segment and its external segment equals the square of the length of the tangent segment.
Power of a point with two secant segments
The segments of a secant segment and a tangent segment which share an endpoint outside of the circle. The product of the lengths of the secant segment and its external segment equals the square of the length of the tangent segment.
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.